Associations among variates and mutual information • inferno

$\newcommand{\mo}{\mathrel{\!=\!}}$

This vignette gives an introduction and guide to the visual and quantitative capabilities and functions of the inferno package, for the study of associations, correlations, and links.

See the vignette('inferno_start') for an introduction to the package. The present vignette continues with the same example and dataset.

Probabilities and associations

The vignette('inferno_start') focuses on the datasets::penguins dataset, and shows how to calculate probabilities of single and joint variates from that dataset; also probabilities conditional on given variates. These probabilities refers to a new unit; for example:

If we find that $\mathrm{Pr}(\text{species}\mo \text{Adelie}) = 44\%$, then there’s a 44% probability that the next penguin we sample (from the same population) is of the Adélie species.
If we find that $\mathrm{Pr}(\text{species}\mo \text{Gentoo} \,\vert\, \text{island} \mo \text{Biscoe}) = 1\%$, then if we have a new penguin, and we know it is from Biscoe island, there’s a 1% probability that it is of the Gentoo species.

And these probabilities can also be interpreted as “estimates” of the corresponding whole-population frequencies.

Joint probabilities and conditional probabilities already give a quantitative measure of the “association”, “correlation”, or “link” between several variates. They tell us for instance that it can be rare or very common to observe particular pairs of values together; or that it is rare or very common to observe values of some variates in cases where other variates have particular values. In the example above, it’s rare to observe the value 'Gentoo' of the variate species in penguins that have value 'Biscoe' for the variate island. These associations are extremely important in fields like medicine, where we may want to diagnose or prognose a disease from possible symptoms, or we try to understand which clinical conditions are associated with the disease, possibly because of underlying biological reasons.

We shall now explore first some visual ways to examine associations with inferno, and then some more precise quantitative ways, which also apply when visualization becomes impossible.

Generating and plotting new samples

Setup

Let’s load the inferno package, if we haven’t already done so, and set a random seed to ensure reproducibility:

library('inferno')

set.seed(10)

As in the vignette('inferno_start'), we work with a specific population of penguins, of which we have 344 sample data stored in the [datasets::penguins] dataset, included in R version 4.5.0 and above. For your convenience you can download the shuffled dataset as the CSV file penguin_data.csv, then load it with the read.csvi() function as follows:

We assume that we have already learned all predictive information from this dataset by means of the inferno function learn(). This information is stored in an object stored in the compressed file learnt.rds within the output directory that was specified in the learn() function. For your convenience the object produced by the computation above can be downloaded as the file learntall.rds. Once you have downloaded it in your working directory you can just invoke

learnt <- 'learntall.rds'

which produces an object learnt (just a character string, in this case) which shall be used in the following analysis.

Generating new samples

Let’s focus on the island and species variates. Each variate has three possible values; inferno’s utility function vrtgrid() allows us to create a vector of all possible values of each variate, which are stored in the metadata of the learnt object:

islandvalues <- vrtgrid(vrt = 'island', learnt = learnt)
# [1] "Biscoe"    "Dream"     "Torgersen"

speciesvalues <- vrtgrid(vrt = 'species', learnt = learnt)
# [1] "Adelie"    "Chinstrap" "Gentoo"

The flexiplot() function allows us to display the island and species variates against each other, for all sample data, as a scatter plot:

flexiplot(x = penguin$island, y = penguin$species,
    type = 'p', xlab = 'island', ylab = 'species',
    xdomain = islandvalues, ydomain = speciesvalues)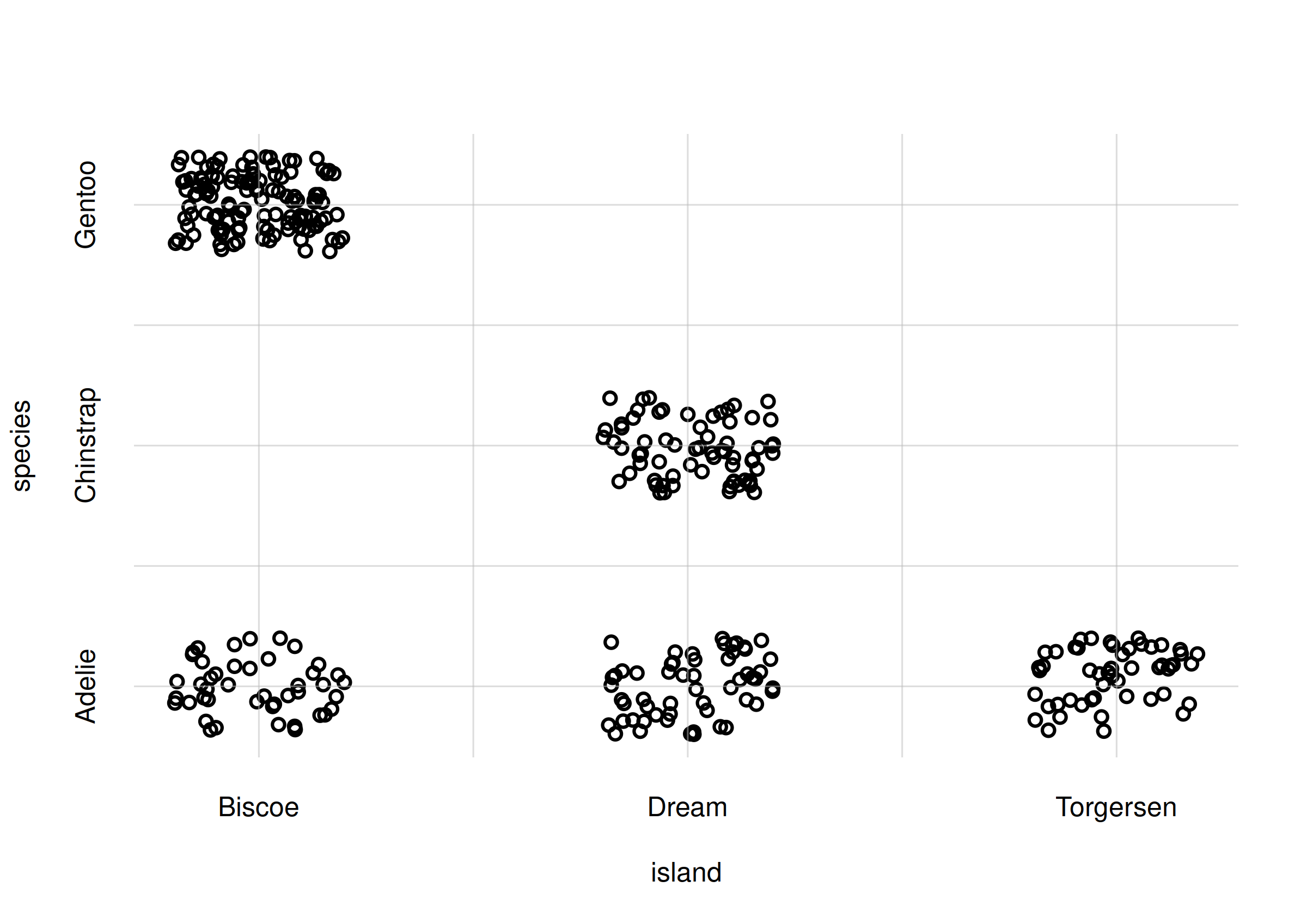

Scatter plot of sample data

Note how flexiplot() automatically add a slight jitter (by means of base::jitter()) to the discrete variates, so that the points don’t just overlap rendering the plot otherwise incomprehensible.

We immediately see some basic features of these variates in this sample. For example:

the most common occurrence is the pair island = 'Biscoe' and species = 'Gentoo';
the pair island = 'Torgersen' and species = 'Chinstrap' does not occur at all.

These are only features of this specific data sample, however. Can we generalize them to the whole population? Intuitively it seems probable that the 'Biscoe'-'Gentoo' pair can indeed be the commonest occurrence in the whole population as well. But we can’t say for sure that the 'Torgersen'-'Chinstrap' pair never occurs in the whole population: our sample included only 344 penguins, so what we can say is that this pair roughly occurs less frequently than once every 344 penguins. In fact, a calculation with the Pr() function shows that its probability is around 0.3%:

prob <- Pr(Y = data.frame(island = 'Torgersen', species = 'Chinstrap'),
    learnt = learnt)

signif(prob$values, digits = 2)
#                      X
# Y                      [,1]
#   Torgersen,Chinstrap 0.003

This example shows the limitations of using sample data for visualizing features of the whole population. How would a scatter plot analogous to the one above look like, for the whole population of for a much larger sample?

The inferno package offers the function rPr() to generate a data.frame of fictitious samples from the estimated frequencies of the whole population. These samples can be used for different purposes, for instance to produce a scatter plot. The main arguments of rPr() are:

n: a positive integer, the number of samples to generate.
Ynames: vector of variate names; samples are generates for these variates jointly.
X: data frame of variate values to restrict the sampling to specific subpopulations.
learnt: the object that points to the computation made with the learn() function.

Let’s first generate 5 samples from the estimated whole population of penguins, as an example:

rPr(
    n = 5,
    Ynames = c('island', 'species'),
    learnt = learnt
)
#        island   species
# 644_1  Biscoe    Gentoo
# 996_1  Biscoe    Gentoo
# 1228_1 Biscoe    Adelie
# 2230_1  Dream Chinstrap
# 3083_1  Dream Chinstrap

The rows of the resulting data frame are named according to the Monte Carlo samples used from the learnt object; they can be useful for peculiar studies but we can completely ignore them in the present case.

Now let’s generate 2000 samples, and then plot them in a scatter plot:

samples <- rPr(n = 2000, Ynames = c('island', 'species'), learnt = learnt)

flexiplot(x = samples$island, y = samples$species,
    type = 'p', xlab = 'island', ylab = 'species',
    xdomain = islandvalues, ydomain = speciesvalues)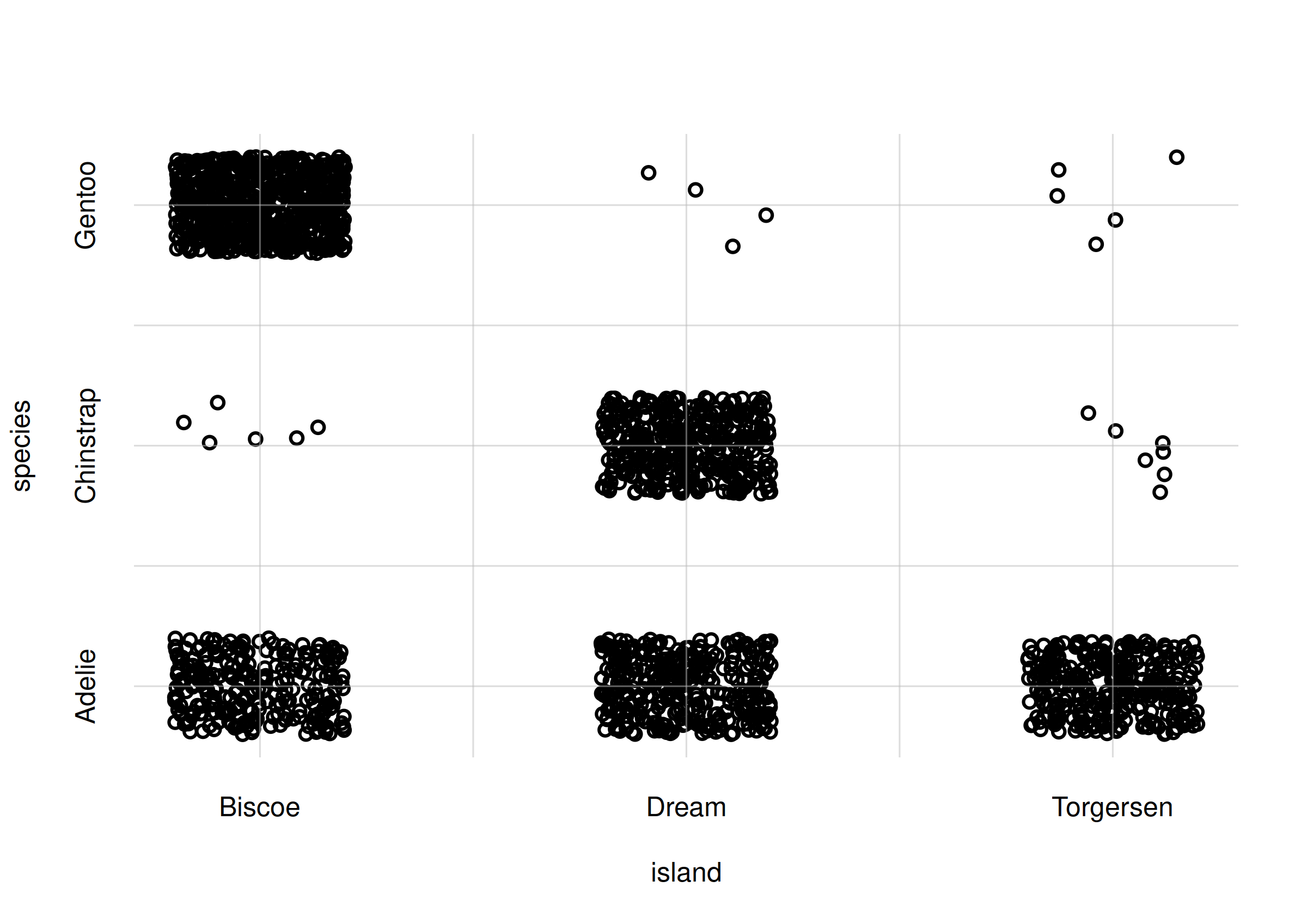

Scatter plot for whole population

The scatter plot above correctly reflects the estimated features of the whole population.

Example with a continuous and a discrete variate

The sampling and plotting from the previous example is easily extended to any other pair or variates, or even to pairs of sets of variates. Let us visualize for instance the joint probability of body_mass and species with another scatter plot.

We generate 2000 whole-population samples of the two variates with rPr(), and then scatter-plot them with flexiplot(). First we select an appropriate plot range for the continuous variate body_mass by means of inferno’s utility function vrtgrid(): this function chooses an optimal value based on, and including, the range of data previously observed:

body_massrange <- range(vrtgrid(vrt = 'body_mass', learnt = learnt))

samples <- rPr(n = 2000, Ynames = c('body_mass', 'species'), learnt = learnt)

flexiplot(x = samples$body_mass, y = samples$species,
    type = 'p', xlab = 'body mass / g', ylab = 'species',
    xlim = body_massrange, ydomain = speciesvalues)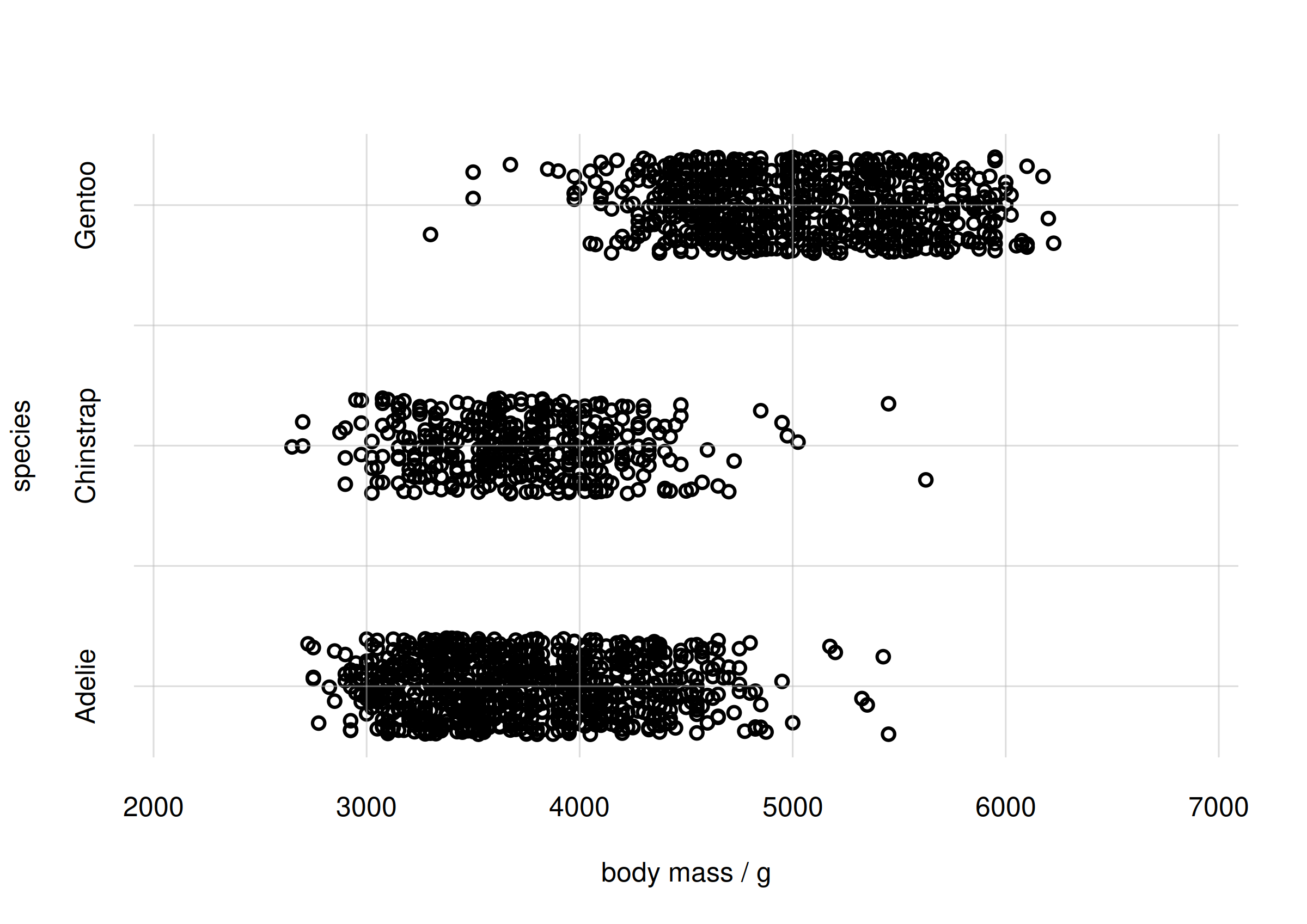

Scatter plot for body mass and species

Note again how flexiplot() automatically add a jitter to the discrete variate species, but not to the continuous body_mass.

From the plot we see that there is an association between the Adélie and Chinstrap species and lighter body mass, around 3500 g; and between the Gentoo species and heavier body mass, around 5000 g. Incidentally, this reflects the probability plot at the end of the vignette('inferno_start').

Samples and plots for different subpopulations

In a completely analogous way we can visually assess the association of two continuous variates, such as body mass and bill length (bill_len):

bill_lenrange <- range(vrtgrid(vrt = 'bill_len', learnt = learnt))

samples <- rPr(n = 2000, Ynames = c('body_mass', 'bill_len'), learnt = learnt)

flexiplot(x = samples$body_mass, y = samples$bill_len,
    type = 'p', xlab = 'body mass / g', ylab = 'bill length / mm',
    xlim = body_massrange, ylim = bill_lenrange)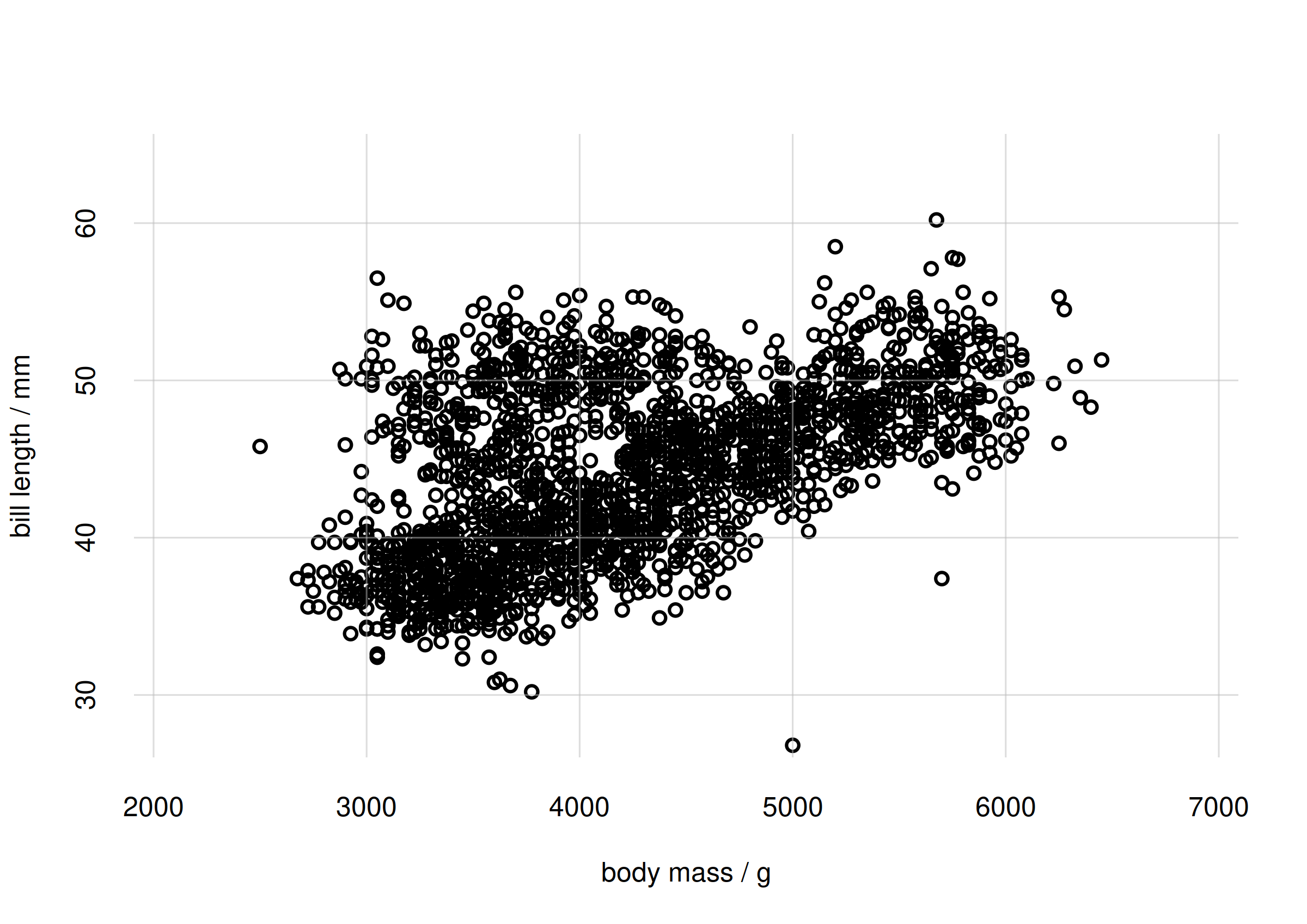

Scatter plot of body mass and bill length

The scatter plot shows that there is a partly linear relationship between body mass and bill length; but there’s a sort of additional cluster around 4000 g for body mass and 45 mm for bill length.

This observation leads to another interesting question: is the association between body_mass and bill_len different for different species? Perhaps the additional cluster is characteristic of one species only. We are therefore interested in studying this association for different subpopulations.

Subpopulation sampling and plots can also be easily done with the rPr() and flexiplot() functions. In the rPr() function we can specify the requested subpopulation via the X argument, analogously to the Pr() function.

Let’s generate sets of samples separately for the species 'Adelie', 'Chinstrap', 'Gentoo':

samplesAdelie <- rPr(
    n = 1000,
    Ynames = c('body_mass', 'bill_len'),
    X = data.frame(species = 'Adelie'),
    learnt = learnt)

samplesChinstrap <- rPr(
    n = 1000,
    Ynames = c('body_mass', 'bill_len'),
    X = data.frame(species = 'Chinstrap'),
    learnt = learnt)

samplesGentoo <- rPr(
    n = 1000,
    Ynames = c('body_mass', 'bill_len'),
    X = data.frame(species = 'Gentoo'),
    learnt = learnt)

Now we plot these samples together with flexiplot(), choosing different colours and shapes for the three subpopulations. We also use the alpha.f argument to make sure that the plot points don’t completely cover one another:

flexiplot(
    x = cbind(samplesAdelie$body_mass,
        samplesChinstrap$body_mass,
        samplesGentoo$body_mass),
    y = cbind(samplesAdelie$bill_len,
        samplesChinstrap$bill_len,
        samplesGentoo$bill_len),
    type = 'p', xlab = 'body mass / g', ylab = 'bill length / mm',
    xlim = body_massrange, ylim = bill_lenrange,
    pch = c(0, 2, 5), col = 2:4, alpha.f = 0.2)

legend('top', speciesvalues, pch = c(0, 2, 5), col = 2:4,
    horiz = TRUE, bty = 'n')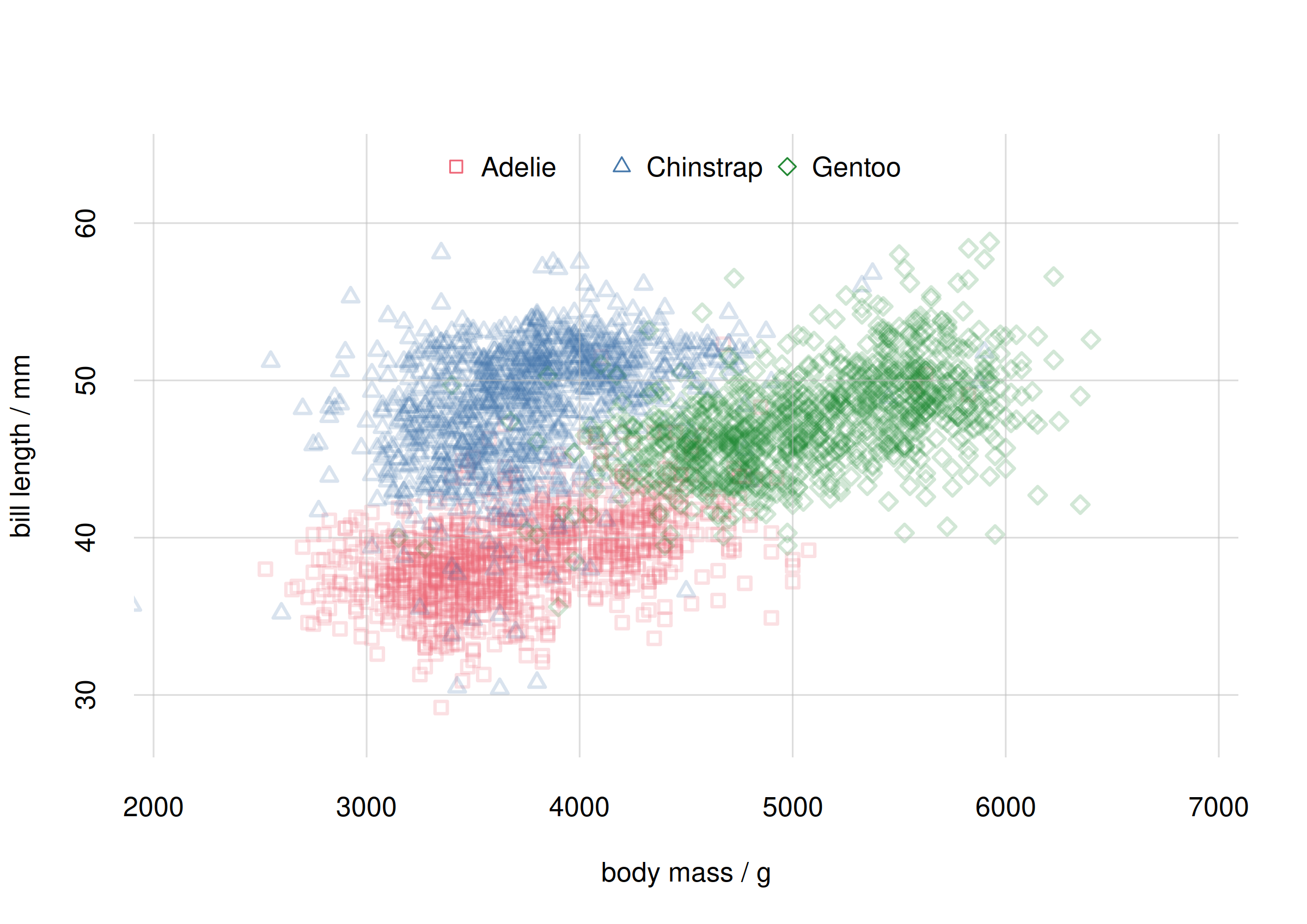

Scatter plot for species subpopulations

The plot above shows quite clearly that the body_mass-bill_len association is indeed different for each species. The roughly linear relationship that we thought we saw earlier was partially spurious, coming from the combination of associations for Adélie and Gentoo penguins.

Quantifying associations and correlations: mutual information

Pearson correlation coefficient and its limitations

Plots like the ones above allow us to explore in a qualitative or semi-quantitative way the associations and correlations between two or three different variates and for different subpopulations. But we would like to quantify associations in a more precise way. And visualization may become impossible when we want to study the association between complex sets of joint variates.

One very common and quite abused measure of “association” is the Pearson correlation coefficient, usually denoted “ $r$ ”. This measure is extremely limited, however. It is essentially based on the assumption that all variates involved have a joint Gaussian distribution. As a consequence, it is a measure of linear association, rather than general association.

For instance, if the distribution of two continuous variates $Y_1$ and $Y_2$ lies in a semicircle, then $Y_2$ is actually a function of $Y_1$ , and is therefore perfectly associated with $Y_1$ : if we know $Y_1$ , then we can exactly predict the value of $Y_2$ . Yet the Pearson correlation coefficient between the two variates is $0$ in this case, simply because the functional dependence of $Y_2$ on $Y_1$ is not linear. Here is an example plot and value:

Y1 <- seq(-1, 1, length.out = 129) ## Y1 values
Y2 <- sqrt(1 - Y1^2) ## Y2 values: function of Y1

## Calculate Pearson correlation coefficient
r <- cor(Y1, Y2, method = 'pearson')
print(r)
# [1] 0

flexiplot(x = Y1, y = Y2, type = 'p',
    xlab = 'Y1', ylab = 'Y2',
    main = paste0('Pearson correlation: ', signif(r, 2)))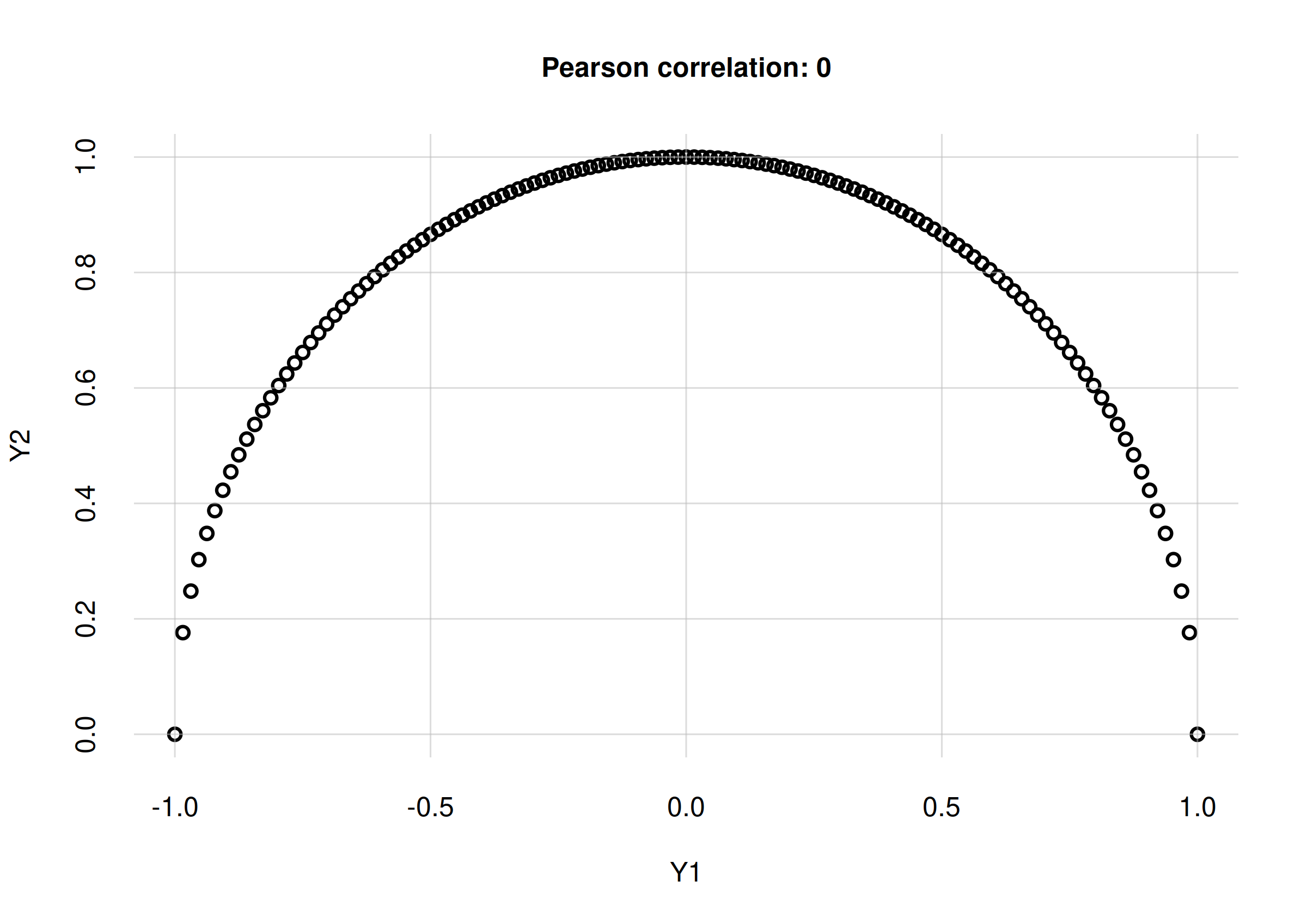

Perfect correlation from $Y_1$ to $Y_2$ , with zero Pearson correlation coefficient

Similar limitations of the Pearson correlation coefficient are demonstrated by the “Anscombe quartet” of datasets.

The Pearson correlation coefficient, moreover, cannot be used in the case of nominal variates, because they cannot be sorted in any meaningful order. Yet there can be clear associations among nominal variates, as was shown for the island and species variates.

Mutual information

Is there a measure of association that enjoys at least the following three properties?:

It quantifies general associations, not just linearity.
It does not make any assumptions (such as Gaussianity) about the distribution of variates.
It can be used for any kind of variates.

The answer is yes, there is! It is called the mutual information or mean transinformation content between variates $Y_1$ and $Y_2$ . It has the following important properties:

If there is no association whatever between $Y_1$ and $Y_2$ , in the sense that knowledge of one never changes our probabilities about the other, then the mutual information between them is zero. Vice versa, if the mutual information is zero, then there is no association of any kind between $Y_1$ and $Y_2$ .
It can be defined for a pair of variates $Y_1$ , $Y_2$ of any kind – continuous, nominal, binary, images, audio signals, and so on.
It is defined for any probability distribution $\mathrm{Pr}(Y_1, Y_2)$ for the two variates, without assumptions such as Gaussian shapes.

Mutual information is always positive or zero, and can be defined in several mathematically equivalent ways, such as the following:

$$ \sum_{y_1, y_2} \mathrm{Pr}(Y_1 \mo y_1, Y_2 \mo y_2) \, \log_{2} \frac{ \mathrm{Pr}(Y_1 \mo y_1, Y_2 \mo y_2) }{ \mathrm{Pr}(Y_1 \mo y_1) \cdot \mathrm{Pr}(Y_2 \mo y_2) } \; \mathrm{Sh} $$

with integrals replacing the sums in the case of continuous variates. It is measured in shannons (symbol $\mathrm{Sh}$ ), or hartleys (symbol $\mathrm{Hart}$ ), or natural units (symbol $\mathrm{nat}$ ). These units and other properties of the mutual information are standardized by the International Organization for Standardization (ISO) and the International Electrotechnical Commission (IEC).

Mutual information is in fact a core quantity of communication theory and information theory. The design and assessment of communication channels depends crucially on it. This makes sense: the main requisite of a communication channel is a strong association between two variates: its input and output messages. You can find a brilliant introduction to its meaning and uses in MacKay’s book, see references.

The inferno package provides the function mutualinfo() to calculate the mutual information between two variates or two sets of joint variates. Its main arguments are the following:

Y1names, Y2names: two vectors of variate names; the mutual information is calculated between these two sets.
X: data frame of variate values to restrict the calculation to specific subpopulations.
learnt: the object that points to the computation made with the learn() function.
Optionally, unit: the mutual information unit; default “shannons” (Sh).
Optionally, parallel specifies how many cores we should use for the computation.

Be aware that the computation can take even tens of minutes if the arguments Y1names and Y2names include multiple joint variates.

Let’s calculate the mutual information between the variates island and species, previously discussed and visualized:

MIislandspecies <- mutualinfo(
    Y1names = 'island', Y2names = 'species',
    learnt = learnt,
    parallel = 4 ## let's use 4 cores
)
# Registered doParallelSNOW with 4 workers
# 
# Closing connections to cores.

The resulting object MIislandspecies is a list of several quantities; the mutual information is given in the $MI element, which includes the accuracy of the result:

MIislandspecies$MI
#    value accuracy 
# 0.621682 0.016000

Between variates island and species there is thus a mutual information of 0.62 Sh. But what does this mean?

Understanding mutual-information values

You might argue: “sure, this mutual information has all these wonderful properties, but what does its value actually mean? I know how to interpret a value of the Pearson correlation coefficient $r$ ”.

It’s important to be fair though. Remember the very first times you learned and used the Pearson correlation coefficient: were you able to give a meaning to “$r = 0.23” for example? was that value high or low? We learned how to interpret $r$ values only through repeated use and application to real situations. The same is true of mutual information: through repeated use and application, you’ll develop an understanding of its possible values.

Mutual information does have an operational meaning. Saying that the mutual information between $X$ and $Y$ is $h\,\mathrm{Sh}$ , means that knowledge of $X$ reduces, on average, $2^h$ times the number of uncertain possibilities of $Y$ . For example suppose that a clinician during a diagnosis is equally uncertain about four possible diseases. There is a particular clinical indicator associated with the disease and the mutual information between the indicator and the disease is $0.415\,\mathrm{Sh}$ . Then, upon testing the clinical indicator, the clinician will be roughly uncertain among three possible diseases, rather than four, because knowledge of the indicator reduces the four possibilities by $2^{0.415}$ ( $4/(2^{0.415}) \approx 3$ ). If the mutual information were $2\,\mathrm{Sh}$ instead, then the indicator would tell the disease with certainty, as it would reduce the four possibilities by $2^{2}$ ( $4/(2^{2}) = 1$ ).

But the function mutualinfo() has an additional output to help you get a rough understanding of the mutual-information value. In the special case of two continuous variates having a joint Gaussian distribution, there is a precise relationship between their mutual information $I$ and their Pearson correlation coefficient $r$ :

$I = -\frac{1}{2} \log_{2}\bigl(1 - r^2\bigr)\;\mathrm{Sh} \,,\qquad \lvert r\rvert = \sqrt{1 - 2^{- 2 I/\mathrm{Sh}}}$

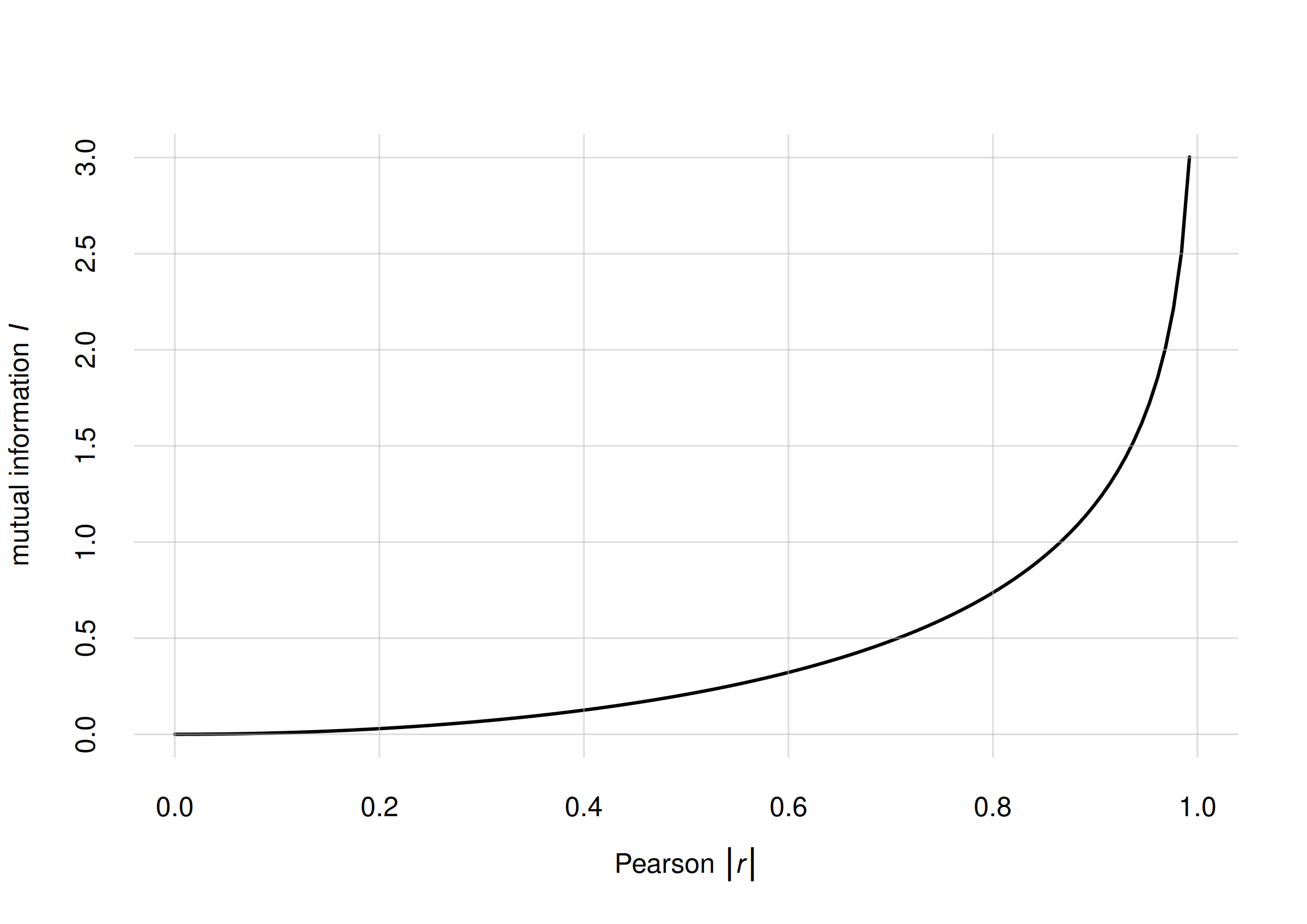
$**$I$ vs $\lvert r\rvert$ for jointly Gaussian variates**$

$I$ vs $\lvert r\rvert$ for jointly Gaussian variates

This relationship can be a rough guide to get familiar with mutual-information values also for non-Gaussian variates. The mutualinfo() function has an additional output element $MI.rGauss$ with the corresponding $\lvert r \rvert$ value. In the previous case of the island and species variates we have

MIislandspecies$MI
#    value accuracy 
# 0.621682 0.016000

MIislandspecies$MI.rGauss
#    value accuracy 
# 0.760009 0.008900

Mutual information for previous examples

Let’s re-display the scatter plots of the three pairs of variates explored previously, and calculate also their mutual information.

Island and species

## mutual info, previously calculated
mi <- signif(MIislandspecies$MI['value'], digits = 2)

## approx r-equivalent
r <- signif(MIislandspecies$MI.rGauss['value'], digits = 2)

samples <- rPr(n = 2000, Ynames = c('island', 'species'), learnt = learnt)

flexiplot(x = samples$island, y = samples$species,
    type = 'p', xlab = 'island', ylab = 'species',
    xdomain = islandvalues, ydomain = speciesvalues,
    main = paste0('mutual info: ', mi, ' Sh',
        '  (rough r-equiv: ', r, ')') )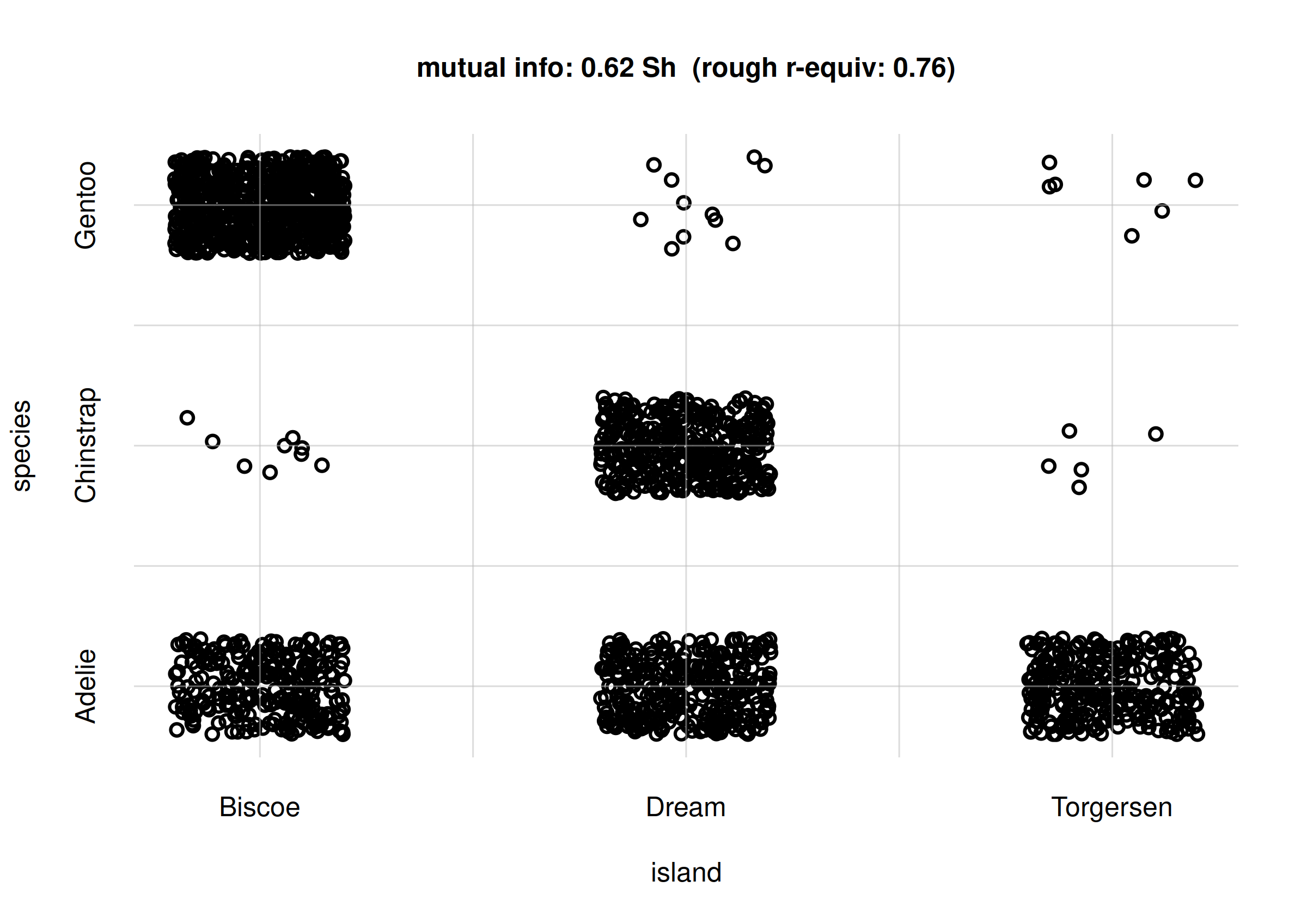

Scatter plot for island and species

Body mass and species

Calculation of mutual info:

MIbodymassspecies <- mutualinfo(
    Y1names = 'body_mass', Y2names = 'species',
    learnt = learnt,
    parallel = 4
)
# Registered doParallelSNOW with 4 workers
# 
# Closing connections to cores.

Scatter plot:

## mutual info
mi <- signif(MIbodymassspecies$MI['value'], digits = 2)

## approx r-equivalent
r <- signif(MIbodymassspecies$MI.rGauss['value'], digits = 2)

samples <- rPr(n = 2000, Ynames = c('body_mass', 'species'), learnt = learnt)

flexiplot(x = samples$body_mass, y = samples$species,
    type = 'p', xlab = 'body mass / g', ylab = 'species',
    xlim = body_massrange, ydomain = speciesvalues,
    main = paste0('mutual info: ', mi, ' Sh',
        '  (rough r-equiv: ', r, ')') )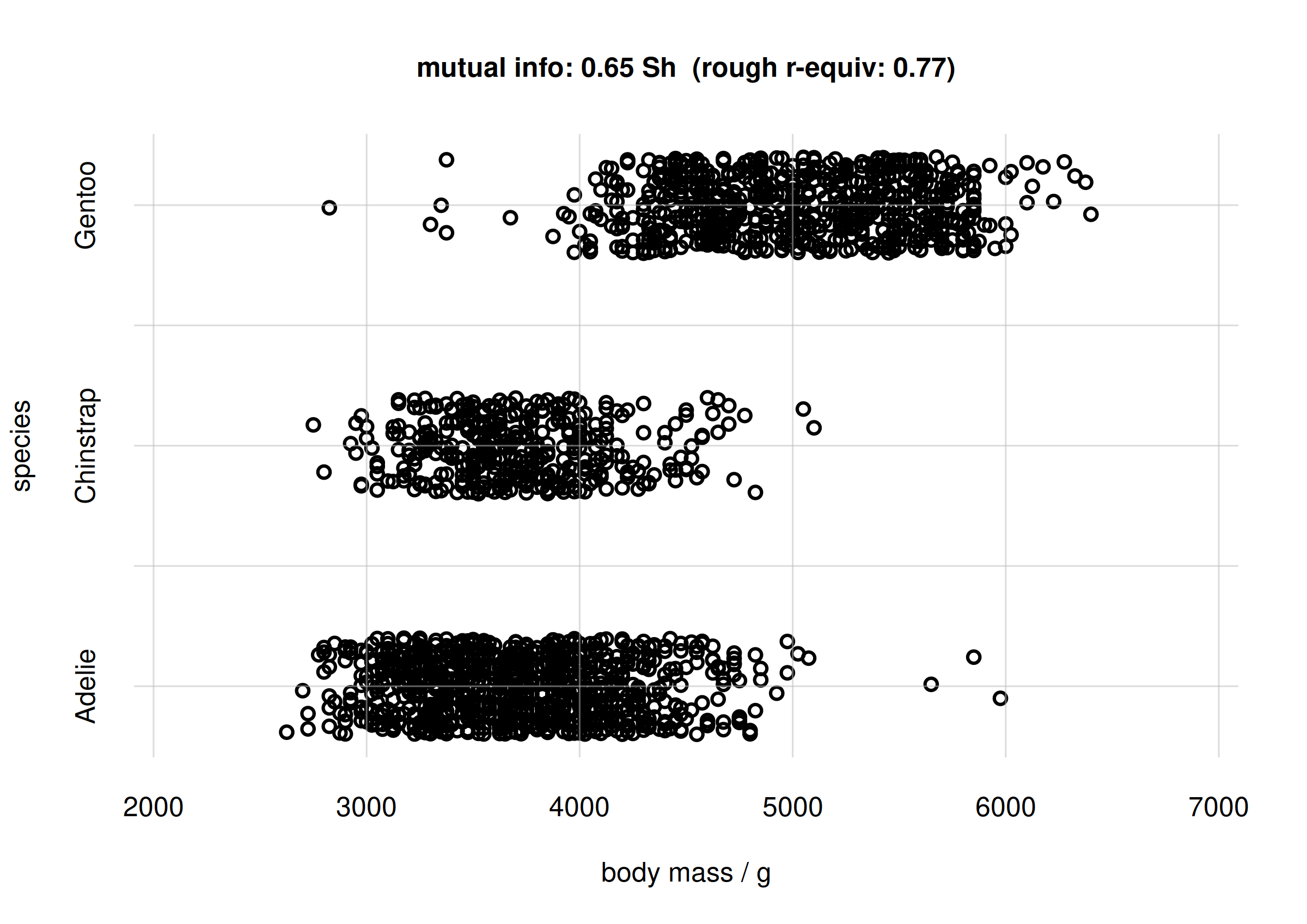

Scatter plot and mutual info for body mass and species

Body mass and bill length

Calculation of mutual information:

MIbodymassbilllen <- mutualinfo(
    Y1names = 'body_mass', Y2names = 'bill_len',
    learnt = learnt,
    parallel = 4
)
# Registered doParallelSNOW with 4 workers
# 
# Closing connections to cores.

Scatter plot:

## mutual info
mi <- signif(MIbodymassbilllen$MI['value'], digits = 2)

## approx r-equivalent
r <- signif(MIbodymassbilllen$MI.rGauss['value'], digits = 2)

samples <- rPr(n = 2000, Ynames = c('body_mass', 'bill_len'), learnt = learnt)

flexiplot(x = samples$body_mass, y = samples$bill_len,
    type = 'p', xlab = 'body mass / g', ylab = 'bill length / mm',
    xlim = body_massrange, ylim = bill_lenrange,
    main = paste0('mutual info: ', mi, ' Sh',
        '  (rough r-equiv: ', r, ')') )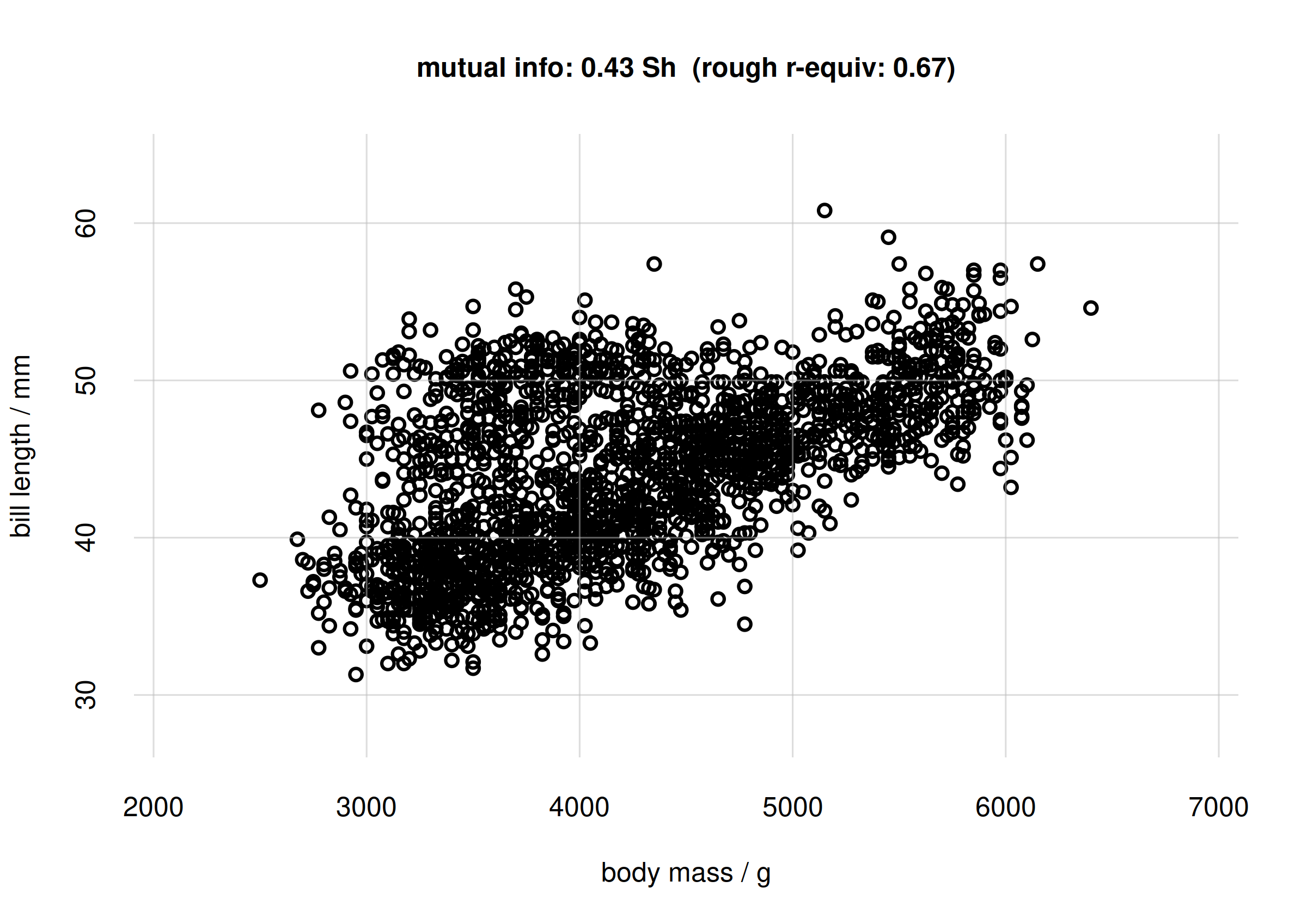

Scatter plot and mutual info for body mass and bill length

Note that in this case the Pearson correlation between body_mass and bill_len is

cor(samples$body_mass, samples$bill_len, method = 'pearson')
# [1] 0.562959

which is different from the rough $r$ -equivalent 0.67.

Mutual information within subgroups

We previously discovered that the association between body mass and bill length is different for different penguin species. The mutualinfo() function allows us to calculate mutual information between two sets of variates within a particular subpopulation. This way we can determine whether two variates are more tightly associated within a particular subpopulation than within another. This kind of studies is important in medicine, where for instance a particular symptom may be a stronger indicator of a disease in a particular subgroup (e.g. females) than in another (e.g. males).

The subpopulation is chosen with the argument X, as in the Pr() and rPr() functions. Let’s calculate the mutual information between body_mass and bill_len within each penguin species (please be aware that the whole computation could take half an hour):

MIadelie <- mutualinfo(
    Y1names = 'body_mass', Y2names = 'bill_len',
    X = data.frame(species = 'Adelie'), ## choose subpopulation
    learnt = learnt,
    parallel = 4
)

MIchinstrap <- mutualinfo(
    Y1names = 'body_mass', Y2names = 'bill_len',
    X = data.frame(species = 'Chinstrap'), ## choose subpopulation
    learnt = learnt,
    parallel = 4
)

MIgentoo <- mutualinfo(
    Y1names = 'body_mass', Y2names = 'bill_len',
    X = data.frame(species = 'Gentoo'), ## choose subpopulation
    learnt = learnt,
    parallel = 4
)

Let’s compare the mutual information between body_mass and bill_len for each species, reporting the result together with the previous scatter plot:

## mutual info, joined
mispecies <- signif(c(
    MIadelie$MI['value'],
    MIchinstrap$MI['value'], 
    MIgentoo$MI['value']
), digits = 2)

flexiplot(
    x = cbind(samplesAdelie$body_mass,
        samplesChinstrap$body_mass,
        samplesGentoo$body_mass),
    y = cbind(samplesAdelie$bill_len,
        samplesChinstrap$bill_len,
        samplesGentoo$bill_len),
    type = 'p', xlab = 'body mass / g', ylab = 'bill length / mm',
    xlim = body_massrange, ylim = bill_lenrange,
    pch = c(0, 2, 5), col = 2:4, alpha.f = 0.2)

legend('top',
    paste(speciesvalues, paste0(mispecies, ' Sh'), sep = ': '),
    pch = c(0, 2, 5), col = 2:4,
    horiz = TRUE, bty = 'n')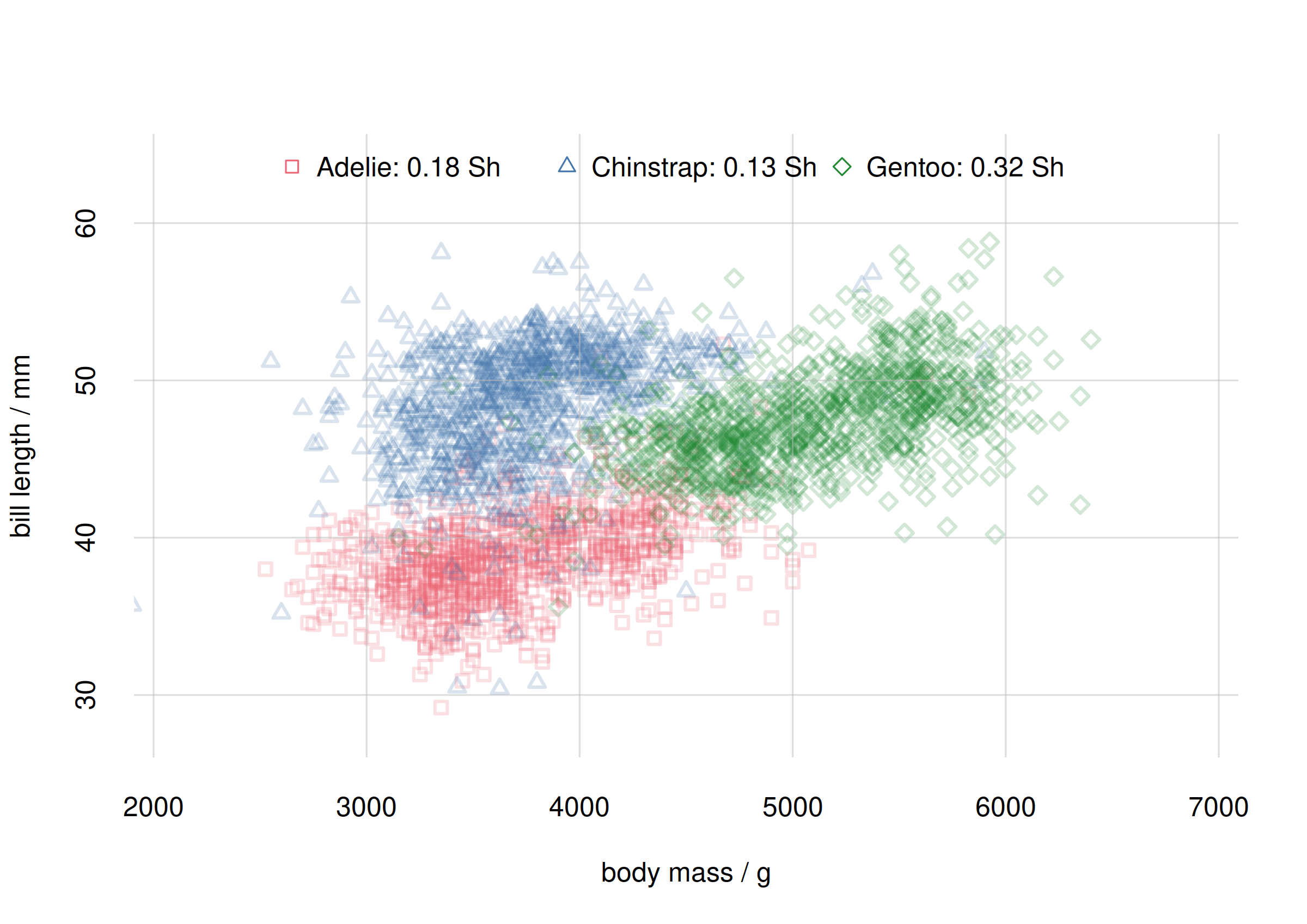

Scatter plot and mutual info for species subpopulations

We see that body mass and bill length have a stronger association in the Gentoo species than in the Adélie or Chinstrap ones. In other words we can more precisely predict body mass from bill length, or vice versa, for Gentoo penguins than for the other two species.

It is interesting to contrast this result with values of the Pearson correlation coefficient:

## Pearson r for Adelie subpopulation:
cor(samplesAdelie$body_mass, samplesAdelie$bill_len, method = 'pearson')
# [1] 0.467353

## Pearson r for Chinstrap subpopulation:
cor(samplesChinstrap$body_mass, samplesChinstrap$bill_len, method = 'pearson')
# [1] 0.352141

## Pearson r for Gentoo subpopulation:
cor(samplesGentoo$body_mass, samplesGentoo$bill_len, method = 'pearson')
# [1] 0.479998

The Pearson correlation yields the same the association ranking as the mutual information does (first Gentoo, then Adélie, then Chinstrap), but it yields the association for the Adélie subpopulation to be closer to the Gentoo one than to the Chinstrap one. The mutual information yields the opposite.

(TO BE CONTINUED)

Appendices

References

MacKay: Information Theory, Inference, and Learning Algorithms (2005).