36  Making decisions

Published

2025-11-29

36.1 Maximization of expected utility

In the previous chapter we associated utilities to consequences, that is, pairs \((\mathsfit{\color[RGB]{204,187,68}D}\mathbin{\mkern-0.5mu,\mkern-0.5mu}{\color[RGB]{238,102,119}Y\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}y})\) of decisions and outcomes. We can also associate utilities to the decisions alone – and these are used to determine the optimal decision.

The expected utility of a decision \(\mathsfit{\color[RGB]{204,187,68}D}\) in a basic decision problem is calculated as a weighted average over all possible outcomes, the weighs being the outcomes’ probabilities:

\[\mathrm{U}(\mathsfit{\color[RGB]{204,187,68}D}\nonscript\:\vert\nonscript\:\mathopen{}\mathsfit{I}) = \sum_{\color[RGB]{238,102,119}y} \mathrm{U}(\mathsfit{\color[RGB]{204,187,68}D}\mathbin{\mkern-0.5mu,\mkern-0.5mu}{\color[RGB]{238,102,119}Y\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}y} \nonscript\:\vert\nonscript\:\mathopen{} \mathsfit{I}) \cdot \mathrm{P}({\color[RGB]{238,102,119}Y\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}y} \nonscript\:\vert\nonscript\:\mathopen{} \mathsfit{\color[RGB]{204,187,68}D}\mathbin{\mkern-0.5mu,\mkern-0.5mu}{\color[RGB]{34,136,51}X\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}x} \mathbin{\mkern-0.5mu,\mkern-0.5mu}\mathsfit{\color[RGB]{34,136,51}data}\mathbin{\mkern-0.5mu,\mkern-0.5mu}\mathsfit{I}) \]


According to Decision Theory the agent’s final decision is determined by the

Principle of maximal expected utility for simple decision problems

The optimal decision which should be made by the agent is the one having maximal expected utility:

\[ \mathsfit{\color[RGB]{204,187,68}D}_{\text{optimal}} = \operatorname{argmax}\limits\limits_{\mathsfit{\color[RGB]{204,187,68}D}} \sum_{\color[RGB]{238,102,119}y} \mathrm{U}(\mathsfit{\color[RGB]{204,187,68}D}\mathbin{\mkern-0.5mu,\mkern-0.5mu}{\color[RGB]{238,102,119}Y\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}y} \nonscript\:\vert\nonscript\:\mathopen{} \mathsfit{I}) \cdot \mathrm{P}({\color[RGB]{238,102,119}Y\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}y} \nonscript\:\vert\nonscript\:\mathopen{} \mathsfit{\color[RGB]{204,187,68}D}\mathbin{\mkern-0.5mu,\mkern-0.5mu}{\color[RGB]{34,136,51}X\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}x} \mathbin{\mkern-0.5mu,\mkern-0.5mu}\mathsfit{\color[RGB]{34,136,51}data}\mathbin{\mkern-0.5mu,\mkern-0.5mu}\mathsfit{I}) \]

where, in some tasks, the probabilities may not depend on \(\mathsfit{\color[RGB]{204,187,68}D}\).

This is also called the principle of expected-utility maximization and other similar names.

In the formula above, “\(\operatorname{argmax}\limits\limits_z G(z)\)” is the value \(z^*\) which maximizes the function \(G(z)\). Note the difference:  \(\max\limits_z G(z)\)  is the value of the maximum itself (its \(y\)-coordinate, so to speak), whereas  \(\operatorname{argmax}\limits\limits_z G(z)\)  is the value of the argument that gives the maximum (its \(x\)-coordinate). For instance

\[\max\limits_z (1-z)^2 = 0 \qquad\text{\small but}\qquad \operatorname{argmax}\limits\limits_z (1-z)^2 = 1\]


It may happen that there are several decisions which have equal, maximal expected utility. In this case any one of them can be chosen. A useful strategy is to choose one among them with equal probability. Such strategy helps minimizing the loss from possible small errors in the specification of the utilities, or from the presence of an antagonist agent which tries to predict what our agent is doing.

Numerical implementation in simple cases

The principle of maximal expected utility is straightforward to implement in many important problems.

In § 35.3 we represented the set of utilities by a utility matrix \(\boldsymbol{\color[RGB]{68,119,170}U}\). If the probabilities of the outcomes do not depend on the decisions, we represent them as a column matrix \(\boldsymbol{\color[RGB]{34,136,51}P}\), having one entry per outcome:

\[ \boldsymbol{\color[RGB]{34,136,51}P}\coloneqq \begin{bmatrix} \mathrm{P}({\color[RGB]{238,102,119}Y\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}y}' \nonscript\:\vert\nonscript\:\mathopen{} {\color[RGB]{34,136,51}X\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}x} \mathbin{\mkern-0.5mu,\mkern-0.5mu}\mathsfit{\color[RGB]{34,136,51}data}\mathbin{\mkern-0.5mu,\mkern-0.5mu}\mathsfit{I}) \\ \mathrm{P}({\color[RGB]{238,102,119}Y\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}y}'' \nonscript\:\vert\nonscript\:\mathopen{} {\color[RGB]{34,136,51}X\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}x} \mathbin{\mkern-0.5mu,\mkern-0.5mu}\mathsfit{\color[RGB]{34,136,51}data}\mathbin{\mkern-0.5mu,\mkern-0.5mu}\mathsfit{I}) \\ \dotso \end{bmatrix} \]

Then the collection of expected utilities is a column matrix, having one entry per decision, given by the matrix product \(\boldsymbol{\color[RGB]{68,119,170}U}\boldsymbol{\color[RGB]{34,136,51}P}\).

All that’s left is to check which of the entries in this final matrix is maximal.

36.2 Concrete example: targeted advertisement

As a concrete example application of the principle of maximal expected utility, let’s keep on using the adult-income task from chapter  33, in a typical present-day scenario.

Some corporation, which offers a particular phone app, wants to bombard its users with advertisements, because advertisement generates much more revenue than making the users pay for the app. For each user the corporation can choose one among three ad-types, let’s call them \({\color[RGB]{204,187,68}A}, {\color[RGB]{204,187,68}B}, {\color[RGB]{204,187,68}C}\). The revenue obtained from these ad-types depends on whether the target user’s income is \({\color[RGB]{238,102,119}{\small\verb;<=50K;}}\) or \({\color[RGB]{238,102,119}{\small\verb;>50K;}}\). A separate study run by the corporation has shown that the average revenues (per user per minute) depending on the three ad-types and the income levels are as follows:

Table 36.1: Revenue depending on ad-type and income level
\(\mathit{\color[RGB]{238,102,119}income}\)
\({\color[RGB]{238,102,119}{\small\verb;<=50K;}}\) \({\color[RGB]{238,102,119}{\small\verb;>50K;}}\)
ad-type \({\color[RGB]{204,187,68}A}\) \(\color[RGB]{68,119,170}-1\,\$\) \(\color[RGB]{68,119,170}3\,\$\)
\({\color[RGB]{204,187,68}B}\) \(\color[RGB]{68,119,170}2\,\$\) \(\color[RGB]{68,119,170}2\,\$\)
\({\color[RGB]{204,187,68}C}\) \(\color[RGB]{68,119,170}3\,\$\) \(\color[RGB]{68,119,170}-1\,\$\)

Ad-type \({\color[RGB]{204,187,68}B}\) is a neutral advertisement type that leads to revenue independently of the target user’s income. Ad-type \({\color[RGB]{204,187,68}A}\) targets high-income users, leading to higher revenue from them; but it leads to a loss if shown to the wrong target (more money spent on making and deploying the ad than what is gained from users’ purchases). Vice versa, ad-type \({\color[RGB]{204,187,68}B}\) targets low-income users, with a reverse effect.

The corporation doesn’t have access to its users’ income levels, but it covertly collects, through some other app, all or some of the eight predictor variates \(\color[RGB]{34,136,51}\mathit{workclass}\), \(\color[RGB]{34,136,51}\mathit{education}\), \(\color[RGB]{34,136,51}\dotsc\), \(\color[RGB]{34,136,51}\mathit{sex}\), \(\color[RGB]{34,136,51}\mathit{native\_country}\) from each of its users. The corporation has also access to the adult-income dataset (or let’s say a more recent version of it).

In this scenario the corporation would like to use an AI agent that can choose and show the optimal ad-type to each user.


Our prototype agent from chapters 31, 32, 33 can be used for such a task. It has already been trained with the dataset, and can use any subset (possibly even empty) of the eight predictors to calculate the probability for the two income levels.

All that’s left is to equip our prototype agent with a function that outputs the optimal decision, given the calculated probabilities and the set of utilities. In our code this is done by the function decide() described in chapter  32 and reprinted here:

decide(probs, utils=NULL)
Arguments:
  • probs: a probability distribution for one or more variates.
  • utils: a named matrix or array of utilities. The rows of the matrix correspond to the available decisions, the columns or remaining array dimensions correspond to the possible values of the predictand variates.
Output:

a list of elements EUs and optimal:

  • EUs is a vector containing the expected utilities of all decisions, sorted from highest to lowest;
  • optimal is the decision having maximal expected utility, or one of them, if more than one, selected with equal probability.
Notes:
  • If utils is missing or NULL, a matrix of the form \(\begin{bsmallmatrix}1&0&\dotso\\0&1&\dotso\\\dotso&\dotso&\dotso\end{bsmallmatrix}\) is assumed (which corresponds to using accuracy as evaluation metric).

Example

A new user logs in; all eight predictors are available for this user:

\[\color[RGB]{34,136,51} \begin{aligned} &\mathit{workclass} \mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}{\small\verb;Private;} && \mathit{education} \mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}{\small\verb;Bachelors;} \\ & \mathit{marital\_status} \mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}{\small\verb;Never-married;} && \mathit{occupation} \mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}{\small\verb;Prof-specialty;} \\ & \mathit{relationship} \mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}{\small\verb;Not-in-family;} && \mathit{race} \mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}{\small\verb;White;} \\ & \mathit{sex} \mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}{\small\verb;Female;} && \mathit{native\_country} \mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}{\small\verb;United-States;} \end{aligned} \]

The agent calculates (using the infer() function) the probabilities for the two income levels, which turn out to be

\[ \begin{aligned} &\mathrm{P}({\color[RGB]{238,102,119}\mathit{\color[RGB]{238,102,119}income}\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}{\color[RGB]{238,102,119}{\small\verb;<=50K;}}} \nonscript\:\vert\nonscript\:\mathopen{} \mathsfit{\color[RGB]{34,136,51}predictor}, \mathsfit{\color[RGB]{34,136,51}data}, \mathsfit{I}) = 83.3\% \\&\mathrm{P}({\color[RGB]{238,102,119}\mathit{\color[RGB]{238,102,119}income}\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}{\color[RGB]{238,102,119}{\small\verb;>50K;}}} \nonscript\:\vert\nonscript\:\mathopen{} \mathsfit{\color[RGB]{34,136,51}predictor}, \mathsfit{\color[RGB]{34,136,51}data}, \mathsfit{I}) = 16.7\% \end{aligned} \]

and can be represented by the column matrix

\[\boldsymbol{\color[RGB]{34,136,51}P}\coloneqq \color[RGB]{34,136,51}\begin{bmatrix} 0.833\\0.167 \end{bmatrix} \]

The utilities previously given can be represented by the matrix

\[\boldsymbol{\color[RGB]{68,119,170}U}\coloneqq \color[RGB]{68,119,170}\begin{bmatrix} -1&3\\2&2\\3&-1 \end{bmatrix} \]

Multiplying the two matrices above we obtain the expected utilities of the three ad-types for the present user:

\[ \boldsymbol{\color[RGB]{68,119,170}U}\boldsymbol{\color[RGB]{34,136,51}P}= \color[RGB]{68,119,170}\begin{bmatrix} -1&3\\2&2\\3&-1 \end{bmatrix} \, \color[RGB]{34,136,51}\begin{bmatrix} 0.833\\0.167 \end{bmatrix}\color[RGB]{0,0,0} = \begin{bmatrix} {\color[RGB]{68,119,170}-1}\cdot{\color[RGB]{34,136,51}0.833} + {\color[RGB]{68,119,170}3}\cdot{\color[RGB]{34,136,51}0.167} \\ {\color[RGB]{68,119,170}2}\cdot{\color[RGB]{34,136,51}0.833} + {\color[RGB]{68,119,170}2}\cdot{\color[RGB]{34,136,51}0.167} \\ {\color[RGB]{68,119,170}3}\cdot{\color[RGB]{34,136,51}0.833} + ({\color[RGB]{68,119,170}-1})\cdot{\color[RGB]{34,136,51}0.167} \end{bmatrix} = \begin{bmatrix} -0.332\\ 2.000\\ \boldsymbol{2.332} \end{bmatrix} \]

The highest expected utility is that of ad-type \({\color[RGB]{204,187,68}C}\), which is therefore shown to the user.

Powerful flexibility of the optimal predictor machine

In the previous chapters we already emphasized and witnessed the flexibility of the optimal predictor machine with regard to the availability of the predictors: it can draw an inference even if some or all predictors are missing.

Now we can see another powerful kind of flexibility: the optimal predictor machine can in principle use different sets of decisions and different utilities for each new application. The decision criterion is not “hard-coded”; it can be customized on the fly.

The possible number of ad-types and the utilities could even be a function of the predictor values. For instance, there could be a set of three ad-types targeting users with \(\color[RGB]{34,136,51}\mathit{education}\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}{\small\verb;Bachelors;}\), a different set of four ad-types targeting users with \(\color[RGB]{34,136,51}\mathit{education}\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}{\small\verb;Preschool;}\), and so on.


36.3 “Unsystematic” decisions

In § 35.6 we emphasized the need to give appropriate utilities to outcomes, and to think about utilities in more general terms or with a more “open mind”, not simply equating them to monetary value, but considering all factors involved.

A similar open mind must be kept in determining the set of available decisions, considering the circumstances and also considering the decisions made by other agents. This leads to the idea of unsystematic decisions, more often called randomized decisions in the literature. Let’s illustrate the idea with an example.

Police Dispatch has received intel that a band of robbers is going to rob either location \(\mathsfit{\color[RGB]{204,187,68}A}\) or location \(\mathsfit{\color[RGB]{204,187,68}B}\). Dispatch can send a patrol to either of these places, but not both, owing to momentarily limited patrolling resources. The police patrol awaits orders from Dispatch on the radio.

Dispatch assigns a utility of, say, \(\color[RGB]{68,119,170}+1\) if the robbery is diverted and possibly the robbers caught, and a utility of \(\color[RGB]{68,119,170}0\) otherwise. As things stand, dispatching the patrol to either location has a 50% probability of catching the robbers, so each location decision has an expected utility of \(\color[RGB]{68,119,170}0.5\). But there’s a catch.

Dispatch has also received intel that the robbers are managing to intercept the radio transmission to the police patrol. So if Dispatch instructs the patrol to “go to location \(\mathsfit{\color[RGB]{204,187,68}A}\)”, the robbers will know that and rob location \(\mathsfit{\color[RGB]{204,187,68}B}\) instead. And vice versa if Dispatch sends the patrol to \(\mathsfit{\color[RGB]{204,187,68}B}\). The updated decision problem has now an expected utility of \(0\) for either choice.

What can Dispatch do? Well there’s at least one more possible decision. Dispatch can radio the patrol and instruct: “Toss a coin; if tails, go to \(\mathsfit{\color[RGB]{204,187,68}A}\); if heads, go to \(\mathsfit{\color[RGB]{204,187,68}B}\)”. If Dispatch does so, then the robbers, even intercepting the radio instruction, can’t to predict for certain where the police patrol will go. Should Dispatch make this third decision?

Exercise 36.1

Draw the diagram for the basic decision problem above, with all three decisions, the outcomes of each, and the corresponding utilities and probabilities.

The third decision, “Toss a coin…” has an expected utility of \(0.5\), whereas the other two, “Go to \(\mathsfit{\color[RGB]{204,187,68}A}\)” or “Go to \(\mathsfit{\color[RGB]{204,187,68}B}\)”, have each \(0\) expected utility. The third decision is optimal among these three.

The crucial feature of the third decision is that it has an element of unpredictability for the robbers; it also has one for Dispatch, but that’s a side-effect.

This idea extends to more complex situations where an agent has an available sequence of decisions, the outcomes of each depending in turn on the decisions of another, antagonist agent. Such a sequence is usually called a strategy. The antagonist agent can in this case manipulate to some degree the outcomes, and alter its own strategy to minimize the first agent’s expected utilities and maximize its own. The first agent can remedy this by introducing a new set of decisions whose outcomes are instead unpredictable to the antagonist (and possibly to itself).

The final decision is not unsystematic or unpredictable

Note that even when we apply such ideas, we are still nevertheless following the principle of maximal expected utility. We haven’t changed or contradicted that principle in any way.

And we are not making decisions “at random”. What we’ve done is simply to consider a different set of decisions; the final choice is never “random”.

To see this, it’s important to make a clear separation between decisions on one side, and objects or results coming from those decisions on the other side. We often make a hasty but incorrect identification of the two. In the police example, there are two locations, \(\mathsfit{\color[RGB]{204,187,68}A}\) and \(\mathsfit{\color[RGB]{204,187,68}B}\), involved. But a location is not a decision – “location \(\mathsfit{\color[RGB]{204,187,68}A}\)” is not even a sentence (recall ch.  6). The initial possible decisions of Dispatch are, properly speaking,

#1. “Say ‘go to location \(\mathsfit{\color[RGB]{204,187,68}A}\)’ on the radio”.
#2. “Say ‘go to location \(\mathsfit{\color[RGB]{204,187,68}B}\)’ on the radio”.

To which then Dispatch adds one more possible decision:

#3. “Say ‘toss a coin; …’ on the radio”.

Dispatch determines that this latter decision #3 has higher expected utility than decisions #1 and #2, and therefore follows it. It isn’t making a decision “at random” among the three possibilities. The final location becomes unpredictable, to Dispatch and to the robbers, but the decision is not unpredictable: it’s #3, determined by maximization of expected utility.

Unfortunately many texts oversimplify this idea, and seem to imply that in some cases it’s best to make decisions “at random”, in apparent contradiction with the principle of maximal expected utility. As we have seen, this is not the case.

It’s also important to emphasize that the unpredictability is desired on the antagonist agent’s side, not on the side of the agent making the decision.


In a decision-making problem, several choices may happen to have equal, maximal expected utilities. In such situations it is usually recommended to “choose randomly” among those choices; this is what the function decide() (§ 36.2) does. This recommendation is an application of the ideas just discussed.

36.4 Multiple decisions: decision trees

Characteristics and graphical representation of a decision tree

In § 2.5 we discussed one important feature of Decision Theory: it can be applied in a sequential, recursive, or modular way. The typical case for such application is when further decisions are available if a specific outcome occurs. It would take several chapters to develop this more general application in full; here we summarize its main features and method.

For the extra curious

Consider a set of decisions and outcomes, which depend on the occurrence of other outcomes and decisions, which in turn may depend on the occurrence of yet more outcomes and decisions, and so on. Graphically this situation can be represented by a decision tree, which depicts the sequences of decisions and outcomes in tree-like fashion. Here is an example:

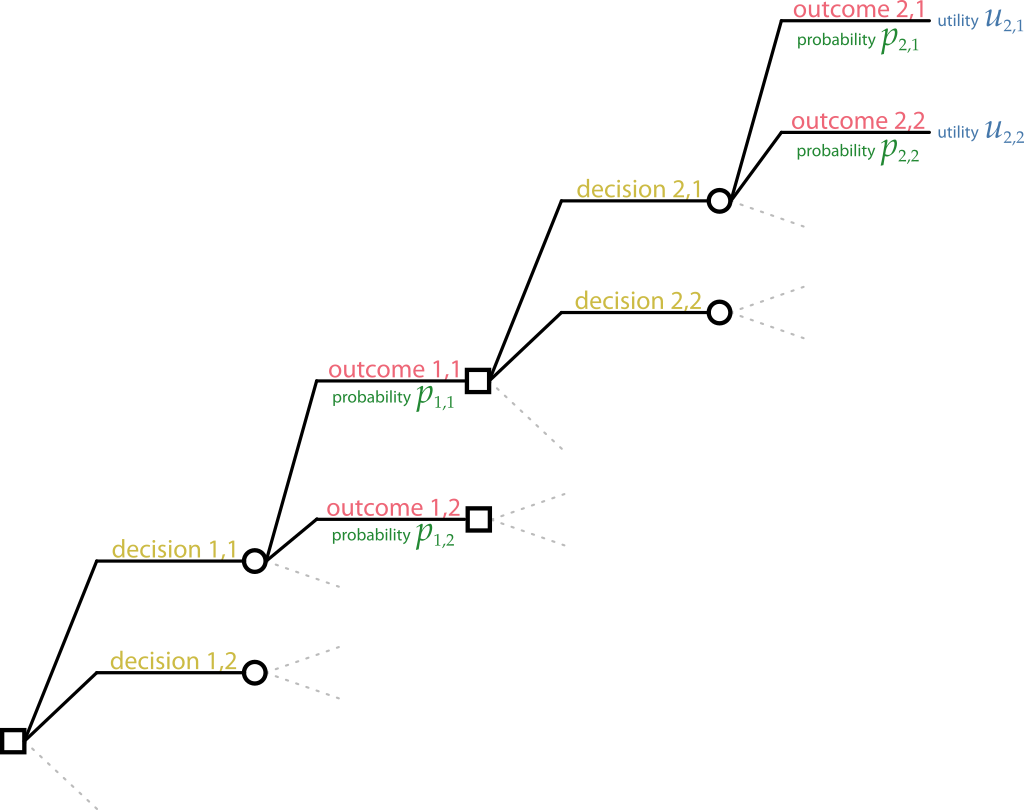
As usual, decision nodes are represented by squares, and inference nodes by circles. The root decision node is on the left. It presents a number of decisions which we can denote

\[\mathsfit{\color[RGB]{204,187,68}D}_{1,1},\quad \mathsfit{\color[RGB]{204,187,68}D}_{1,2},\quad\dotsc,\quad\mathsfit{\color[RGB]{204,187,68}D}_{1,\dotsc},\quad\dotsc\]

The first index  “\({}_{1,}\)”  indicates that these are root decisions; the second index enumerates these decisions. Each decision has a set of possible outcomes which we can denote, all together,

\[\mathsfit{\color[RGB]{34,136,51}O}_{1,1},\quad \mathsfit{\color[RGB]{34,136,51}O}_{1,2},\quad\dotsc,\quad\mathsfit{\color[RGB]{34,136,51}O}_{1,\dotsc},\quad\dotsc\]

with the same indexing convention. Each outcome has an associated degree of belief, which generally depends on the outcome and on the respective decision. For instance, the probability for outcome \(\mathsfit{\color[RGB]{34,136,51}O}_{1,1}\) must be written

\[\mathrm{P}(\mathsfit{\color[RGB]{34,136,51}O}_{1,1} \nonscript\:\vert\nonscript\:\mathopen{} \mathsfit{\color[RGB]{204,187,68}D}_{1,1} \mathbin{\mkern-0.5mu,\mkern-0.5mu}\mathsfit{I})\]

where \(\mathsfit{I}\) is the agent’s background information.

So far this looks almost like a basic decision tree (§ 3.1). Why “almost”? because we don’t associate utilities to these outcomes. Not yet. Instead, we see that some outcomes, like \(\mathsfit{\color[RGB]{34,136,51}O}_{1,1}\), open new decision nodes, with associated outcomes. We can keep the same notation convention as for the root decision node, but now using  “\({}_{2,}\)”  as first index:

\[\mathsfit{\color[RGB]{204,187,68}D}_{2,1},\quad \mathsfit{\color[RGB]{204,187,68}D}_{2,2},\quad\dotsc,\quad\mathsfit{\color[RGB]{204,187,68}D}_{2,\dotsc},\quad\dotsc\]

and for the their outcomes as well:

\[\mathsfit{\color[RGB]{34,136,51}O}_{2,1},\quad \mathsfit{\color[RGB]{34,136,51}O}_{2,2},\quad\dotsc,\quad\mathsfit{\color[RGB]{34,136,51}O}_{2,\dotsc},\quad\dotsc\]

Note that this is just a notation we use here; you can use any other convenient notation you like.

Each outcome of the second level has an associated degree of belief. Note that the degree of belief in an outcome generally depends on all previous decisions and outcomes leading to that outcome. For instance, the probability for outcome \(\mathsfit{\color[RGB]{34,136,51}O}_{2,2}\) must be written

\[\mathrm{P}(\mathsfit{\color[RGB]{34,136,51}O}_{2,2} \nonscript\:\vert\nonscript\:\mathopen{} \mathsfit{\color[RGB]{204,187,68}D}_{2,1} \mathbin{\mkern-0.5mu,\mkern-0.5mu}\mathsfit{\color[RGB]{34,136,51}O}_{1,1} \mathbin{\mkern-0.5mu,\mkern-0.5mu}\mathsfit{\color[RGB]{204,187,68}D}_{1,1} \mathbin{\mkern-0.5mu,\mkern-0.5mu}\mathsfit{I})\]

What about utilities? In this particular decision tree, the outcomes \(\mathsfit{\color[RGB]{34,136,51}O}_{2,1}\) and \(\mathsfit{\color[RGB]{34,136,51}O}_{2,2}\) do not lead to any subsequent possible decisions: they are among the tips of the tree. Then we do associate utilities to them: utilities are only associated to all outcomes at the tips of the decision tree. And it’s important to note that the utility associated to an outcome generally depends on all previous decisions and outcomes leading to that outcome. For instance, the utility associated to outcome \(\mathsfit{\color[RGB]{34,136,51}O}_{2,2}\) must be written

\[\mathrm{U}(\mathsfit{\color[RGB]{204,187,68}D}_{1,1} \mathbin{\mkern-0.5mu,\mkern-0.5mu}\mathsfit{\color[RGB]{34,136,51}O}_{1,1} \mathbin{\mkern-0.5mu,\mkern-0.5mu}\mathsfit{\color[RGB]{204,187,68}D}_{2,1} \mathbin{\mkern-0.5mu,\mkern-0.5mu}\mathsfit{\color[RGB]{34,136,51}O}_{2,2} \nonscript\:\vert\nonscript\:\mathopen{}\mathsfit{I})\]

Let’s summarize these important features of a general decision tree:

Characteristics of a decision tree

  • Some outcomes lead to further decision nodes with associated outcomes.

  • Degrees of belief are associated to each outcome. The degree of belief in an outcome generally depends on all previous decisions and outcomes leading to that outcome.

  • Utilities are associated to outcomes at the tips (not to intermediate ones). The utility associated to an outcome generally depends on all previous decisions and outcomes leading to that outcome.

  • At each level of the tree, it may happen that some outcomes lead to further decisions, while other outcomes are tips.

Decision making with a decision tree

Now to the important question: how do we choose the optimal decision at each decision node? The procedure, which is quite intuitive once one understands its general principle, is called averaging out and folding back or backwards induction. It starts from the tips, and step-wise associates a utility to each decision and each outcome, moving from the tips to the root of the decision tree:

Backwards induction

  1. Take all outcomes at the **tips* which originate from the same inference node (circle).

    At that inference node, calculate the expected utility, using the probabilities and utilities associated with the tip outcomes.

    Note that this inference node stems from a particular decision. The calculated expected utility is associated to that decision.

  2. Repeat the previous step until all tip outcomes have been exhausted.
     

  3. Take all decisions which have an associated expected utility (at the corresponding inference node), and which originate from the same decision node (square).

    At that decision node, calculate the maximal expected utility among the expected utilities of the decisions originating at that node.

    Note that this decision node stems from a particular outcome. The calculated maximal expected utility is associated to that outcome.

  4. Repeat the previous step until all outcomes closest to tip outcomes have been exhausted.
     

Now we have that some outcomes which initially didn’t have any associated utility, because they were not tips of the decision tree, have obtained an associated utility.

Starting from these, repeat the four steps above, and so on recursively. In the end you arrive at the association of expected utilities to all decisions originating from the root decision node.

A concrete example will be added

Misunderstandings and misuses of backwards induction

It’s important to be aware of some characteristics and consequences of backwards induction. Misunderstanding of these is often the origin of misapplications and misunderstandings of this basic method of Decision Theory.

Outcome utilities may depend on outcome frequencies

We have seen that the utility of a final outcome depends on the whole sequence of decisions and outcomes leading to it. This means that such utility may depend on the frequencies with which particular outcomes occur in that sequence. These are objectively observable frequencies, not degrees of beliefs, so there is no contradiction with the basic principle that the utility of an outcome cannot depend on the probability for that outcome.

Some people confuse or simplify a sequential decision problem with a basic decision, trying to interpret the frequencies of the sequence as probabilities in the basic decision. Then they declare that the basic principle of Decision Theory – that the utility of an outcome cannot depend on the degree of belief on that outcome – is broken. Their erroneous conclusion comes from a double error: (1) they confuse a sequential problem with a basic one; (2) they confuse frequencies with degrees of belief.

Utilities need not be additive

We have seen that utilities are associated only to the outcomes at the tip of the decision tree. So the utility is a property of the whole history leading to that outcome, so to speak. In some situations this history may include outcomes that are similar, in some sense, to the final outcome. For example, in a problem of 100 sequential coin bets and tosses, the final outcome might be heads, preceded by a sequence of 44 heads and 55 tails.

In such situations, some people associate a utility to heads and one to tails, and then consider the utility of a sequence leading to 45 heads and 55 tails to be the sum of 45 heads-utilities and 55 tails-utilities. But Decision Theory does not say that the final utility should be calculated this way. In fact, Decision Theory does not even associate any utility to intermediate outcomes; only to the whole history. The summing procedure above is only a special assumption, which may be valid or reasonable in some cases, but unreasonable and invalid in others.


So be careful in your decision analyses; do not take shortcuts or make erroneous simplifications!

36.5 The full extent of Decision Theory

The simple decision-making problems and framework that we have discussed in these notes are only the basic blocks of Decision Theory. This theory covers more complicated decision problems. We only mention some examples:

For the extra curious

Full accounts of Decision Theory can for example be found in:

  • Sequential decisions. Many decision-making problems involve sequences of possible decisions, alternating with sequences of possible outcomes. These sequences can be represented as decision trees. Decision theory allows us to find the optimal decision sequence for instance through the “averaging out and folding back” procedure.


  • Uncertain utilities. It is possible to recast Decision Theory and the principle of maximal expected utility in terms, not of utility functions \(\mathrm{U}(\mathsfit{\color[RGB]{204,187,68}D}\mathbin{\mkern-0.5mu,\mkern-0.5mu}{\color[RGB]{238,102,119}Y\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}y} \nonscript\:\vert\nonscript\:\mathopen{} \mathsfit{I})\), but of probability distributions over utility values:

    \[\mathrm{P}({\color[RGB]{68,119,170}U\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}u} \nonscript\:\vert\nonscript\:\mathopen{} \mathsfit{\color[RGB]{204,187,68}D}\mathbin{\mkern-0.5mu,\mkern-0.5mu}{\color[RGB]{238,102,119}Y\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}y} \mathbin{\mkern-0.5mu,\mkern-0.5mu}\mathsfit{I})\]

    Formally the two approaches can be shown to be equivalent.

For the extra curious


  • Acquiring more information. In many situations the agent has one more possible choice: to gather more information in order to calculate sharper probabilities, rather than deciding immediately. This kind of decision is also accounted for by Decision Theory, and constitutes one of the theoretical bases of “reinforcement learning”.
For the extra curious


  • Multi-agent problems. To some extent it is possible to consider situations (such as games) with several agents having different and even opposing utilities. This area of Decision Theory is apparently still under development.
For the extra curious