12 Quantities and data types
\[ \DeclarePairedDelimiters{\set}{\{}{\}} \DeclareMathOperator*{\argmax}{argmax} \]
Motivation for the “Data I” part
In the “Inference I” part we surveyed the four fundamental rules of inference, which determine how the degrees of belief of an agent should propagate and be mutually consistent, and we explored some of their consequences and applications. The rules can be used with any sentences whatsoever, so their application can be developed in detail in a wide variety of directions, with applications ranging from robotics to psychology. Each of these possible developments would require a full university course by itself.
We shall now restrict our attention to applications typical of engineering, data science, and machine learning, such as classification, forecast, prognosis, and hypothesis testing, in situations that involve quantifiable and measurable phenomena. For this purpose we focus on sentences of particular kinds, which can express such quantification and measurement. In a sense, we develop a specialized “language” for this kind of situations.
Still, since we’re dealing with sentences, the probability calculus and inference rules apply without changes of any kind.
12.1 Quantities
Quantities, values, domains
Most decisions and inferences in engineering and data science involve things or properties of things that we can measure. We represent them by mathematical objects – most often, collections of numbers – with particular mathematical properties and operations.
The mathematical properties reflect the kind of activities that we can do with these things. For instance, colours are represented by particular tuples of numbers, and these tuples can be multiplied by some numeric weights and added, to obtain another tuple. This mathematical operation represents the fact that colours can be obtained by mixing other colours in different proportions. Physics and engineering are founded on this approach.
25% #FF0000 + 75% #0000FF = #4000C0
It’s difficult to find a general term to denote any instance of such “things” and their mathematical representation. Yet it’s convenient if we find one, so we can discuss the general theory without getting bogged down in individual cases. To this purpose we’ll borrow the term quantity from physics and engineering.
We distinguish between a quantity and its value. For instance, a quantity could be “The temperature at the point with coordinates 60.3775029, 5.3869233, 643, at time 1895-10-04T10:03:14Z”; and its value could be \(24\,\mathrm{°C}\).
This distinction is necessary in inference and decision problems, because we may not know the value of a particular quantity. We then consider every possible value that quantity could have, and we can assign a probability to each. The set of possible values is called the domain of the quantity. In our temperature example, the domain is the set of all possible temperatures from \(0\,\mathrm{K}\) and above.
Another example:
- quantity: the image taken by a particular camera at a particular time, represented by a specific collection of numbers (say 128 × 128 × 3$ integers between \(0\) and \(255\))
- values: one possible value is this:
(corresponding to a grid of 128 × 128 × 3 specific numbers), another possible value is this: 
, and there are many other possible values - domain: the collection of \(256^{3\times128\times128} \approx 10^{118 370}\) possible images (corresponding to the collection of possible grids of numeric values)
Other examples of quantities and domains:
The distance between two objects in the Solar System at a specific time. The domain could be, say, all values from \(0\,\mathrm{m}\) to \(6\cdot10^{12}\,\mathrm{m}\) (Pluto’s average orbital distance).
The number of total views of some online video (at a specific time), with a domain, say, from 0 to 20 billions.
The force on an object (at a specific time and place). The domain could be, say, 3D vectors with components in \([-100\,\mathrm{N},\,+100\,\mathrm{N}]\).
The degree of satisfaction in a customer survey, with five possible values
Not at all satisfied,Slightly satisfied,Moderately satisfied,Very satisfied,Extremely satisfied.The graph representing a particular social network. Individuals are represented by nodes, and different kinds of relationships by directed or undirected links between nodes, possibly with numbers indicating their strength. The domain consists of all possible graphs with, say, \(0\) to \(10000\) nodes and all possible combinations of links and weights between the nodes.
The relationship between the input voltage and output current of an electric component. The domain could be all possible continuous curves from \([0\,\mathrm{V}, 10\,\mathrm{V}]\) to \([0\,\mathrm{A}, 1\,\mathrm{A}]\).
A 1-minute audio track recorded by a device with a sampling frequency of 48 kHz (that is, 48 000 audio samples per second). The domain could be all possible sequences of 2 880 000 numbers in \([0,1]\).
The subject of an image, with domain of three possible values
cat,dog,something else.The roll, pitch, yaw of a rocket (at a specific time and place), with domain \((-180°,+180°]\times(-90°,+90°]\times(-180°,+180°]\).
The vague term “data” typically means the values of a collection of quantities.
In these notes we agree that a quantity has one, and only one, value.
Notation
We shall denote quantities by italic letters, such as \(X\), or \(U\), or \(A\). The sentences that appear in decision-making and inferences are therefore often of the kind “the quantity \(X\) was observed to have value \(x\)”, where “\(x\)” stands for a specific value, for instance . This kind of sentences are often abbreviated in the form “\(X\mathclose{}\mathord{\nonscript\mkern 0mu\textrm{\small=}\nonscript\mkern 0mu}\mathopen{}x\)”.
12.2 Basic types of quantities
As the examples above show, quantities and data come in all sorts and with different degrees of complexity. There is no clear-cut divide between different sorts of quantities. The same quantity can moreover be viewed and represented in many different ways, depending on the specific context, problem, purpose, and background information.
It is possible, however, to roughly differentiate between a handful of basic types of quantities, from which more complex types are built. Here is one kind of differentiation that is useful for inference problems about quantities:
Nominal
A nominal or categorical quantity has a domain with a discrete and usually finite number of values. The values are not related by any mathematical property, and do not have any specific order.
This means that it does not make sense to say, for instance, that some value is “twice” or “1.5 times” another, or “larger” or “later” than another one. Nor does it make sense to “add” two quantities. In particular, there is no notion of cumulative probability, quantile, median, average, or standard deviation for a nominal quantity.
Examples: the possible breeds of a dog, or the characters of a film.
It is of course possible to represent the values of a nominal quantity with numbers; say 1 for Dachshund, 2 for Labrador, 3 for Dalmatian, and so on. But that doesn’t mean that
Dalmatian\({}-{}\)Labrador\({}={}\)Labrador\({}-{}\)Dachshund
(just because \(3-2=2-1\)) or similar nonsense.
Ordinal
An ordinal quantity has a domain with a discrete and usually finite number of values. The values are not related by any mathematical property, but they do have a specific order.
This means that it does not make sense to say that some value is “twice” or “1.5 times” another, and we cannot add or subtract two values. But it does make sense to say, for any two values, which one has higher rank, for example “stronger”, or “later”, “larger”, and similar. Owing to the ordering property, it does make sense to speak of cumulative probability, quantile, and median of an ordinal quantity; but there is no notion of average or standard deviation for an ordinal quantity.
Example: a pain-intensity scale. A patient can say whether some pain is more severe than another, but it isn’t clear what a pain “twice as severe” as another would mean (although there’s a lot of research on more precise quantification of pain). Another example: the “strength of friendship” in a social network. We can say that we have a “stronger friendship” with a person than with another; but it doesn’t make sense to say that we are “four times stronger friends” with a person than with another.
It is possible to represent the values of an ordinal quantity with numbers which reflect the order of the values. But it’s important to keep in mind that differences or averages of such numbers do not make sense. For this reason the use of numbers can be misleading at times; a less misleading possibility is to represent ordered values by alphabet letters, for example.
Binary
A binary or dichotomous quantity has only two possible values. It can be seen as a special case of a nominal or ordinal quantity, but the fact of having only two values lends it some special properties in inference problems. This is why we list it separately.
Obviously it doesn’t make much sense to speak of the difference or average of the two values; and their ranking is trivial even if it makes sense.
There’s an abundance of examples of binary quantities: yes/no answers, presence/absence of something, and so on.
Interval
An interval quantity has a domain that can be discrete or continuous, finite or infinite. The values do admit some mathematical operations, at least convex combination and subtraction. They also admit an ordering.
This means that we can say, at the very least, whether the interval or “distance” between a pair of values is the same, or larger, or smaller than the interval between another pair. For this reason we can also say whether a value is larger than another. We can also take weighted sums of values, called convex combinations (keep in mind that simple addition of values may be meaningless for some quantities).
Owing to these mathematical properties, it does make sense to speak of the cumulative probability, quantile, median, and also average and standard deviation for an interval quantity.
The number of electronic components produced in a year by an assembly line is an example of a discrete interval quantity. The power output of a nuclear plant at a given time is an example of a continuous interval quantity.
It is also possible to speak of ratio quantities, which are a special case of interval quantities, but we won’t have use of this distinction in the present notes.
How to decide the basic type of a quantity?
To attribute a basic type to a quantity we must ultimately check how that quantity is defined, obtained, and used. In some cases the values of the quantity may give some clue; for example, if we see values “\(2.74\)”, “\(8.23\)”, “\(3.01\)”, then the quantity is probably of the interval kind. But if we see values “\(1\)”, “\(2\)”, “\(3\)”, it’s unclear whether the quantity is interval, ordinal, nominal, or maybe of yet some other kind.
The type of a quantity also depends on its use in the specific problem. A quantity of a more complex type can be treated as a simpler type if needed. For instance, the response time of some device is in principle an interval quantity (measured, say, in seconds, as precisely as we want); but in a specific situation we could simply label its values as slow, medium, fast, thus turning it into an ordinal quantity.
@@ TODO: add examples for image spaces
12.3 Other attributes of basic types
It is useful to consider other basic aspects of quantities that are somewhat transversal to “type”. These aspects are also important when drawing inferences.
Discrete vs continuous
Nominal and ordinal quantities have discrete domains. The domain of an interval quantity can be discrete or continuous. In practice all domains are discrete, since we cannot observe, measure, report, or store values with infinite precision. In a modern computer, for example, a real number can “only” take on \(2^{64} \approx 20 000 000 000 000 000 000\) possible values. In many situations the available precision is so high that we can consider the quantity as continuous for all practical purposes and use the mathematics of continuous sets – derivation, integration, and so on – to our advantage.
Bounded vs unbounded
Ordinal and interval quantities may have domains with no minimum value, or no maximum value, or neither. Typical terms for these situations are lower- or upper-bounded, or left- or right-bounded, and unbounded; or similar terms.
Whether to treat a quantity domain as bounded or unbounded depends on the quantity, the specific problem, and the computational resources. For example, the number of times a link on a webpage has been clicked can in principle be (right-)unbounded. Another example is the distance between two objects: we can consider it unbounded, but in concrete problems might be bounded, say, by the size of a laboratory, or by Earth’s circumference, or the Solar System’s extension, and so on.
Finite vs infinite
The domain of a discrete quantity can consist of a finite or – at least in theory – an infinite number of possible values (the domain of a continuous quantity always has an infinite number of values). A domain can be infinite and yet bounded: consider the numbers in the range \([0,1]\).
Whether to treat a domain as finite or infinite depends on the quantity, the specific problem, and the computational resources. For example, the intensity of a base colour in a pixel of a particular image might really take on 256 discrete steps between \(0\) and \(1\): \(0, 0.0039215686, 0.0078431373, \dotsc, 1\). But in some situations we can treat this domain as practically infinite, with any possible value between \(0\) and \(1\).
Rounded
A continuous interval quantity may be rounded, owing to the way it’s measured. In this case the quantity could be considered discrete rather than continuous. Rounding can impact the way we do inferences about such a quantity.
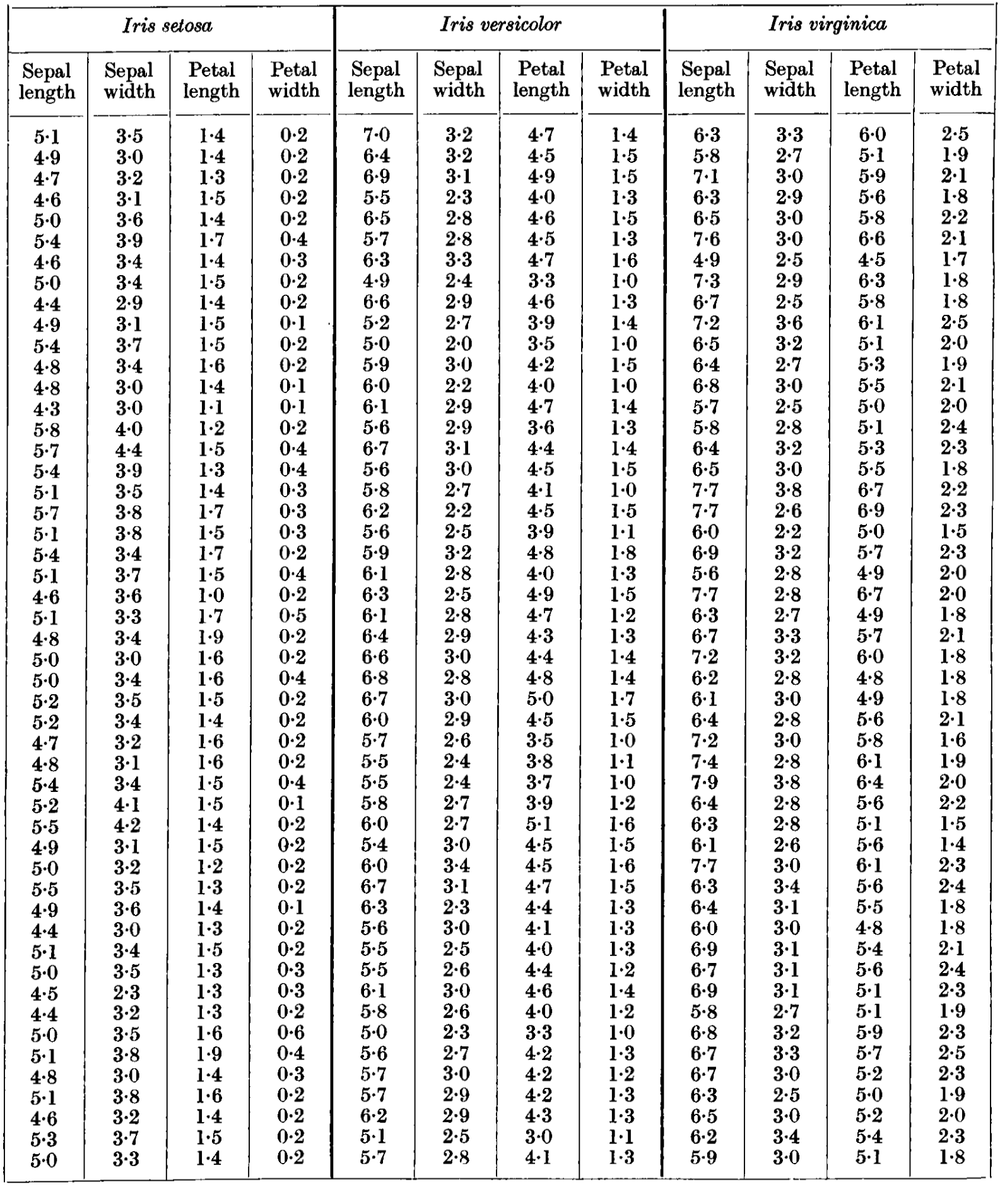The Iris dataset from its original paper
The famous Iris dataset, for instance, consists of several lengths – continuous interval quantities – of parts of flowers. All values are rounded to the millimetre, even if in reality the lengths could have intermediate values, of course. The age of a person is another frequent example of an in-principle continuous quantity which is rounded, say to the year or the month.
In some situations it’s important to be aware of rounding, because it can lead to quantities with different unrounded values to have identical rounded ones.
Censored
The measurement procedure of a quantity may have an artificial lower or upper bound. A clinical thermometer, for instance, could have a maximum reading of \(45\,\mathrm{°C}\). If we measure with it the temperature of a \(50\,\mathrm{°C}\)-hot body, we’ll read “\(45\,\mathrm{°C}\)”, not the real temperature.
A quantity with this characteristic is called censored, more specifically left-censored or right-censored when there’s only one artificial bound. The bound is called the censoring value.
A censoring value denotes an actual value that could also be greater or less. This is important when we draw inferences about this kind of quantities.
12.4 “True” vs “measured” values
A difference is often drawn, especially in physics and engineering, between the “true” value of a quantity and the value “measured” or “observed” with a particular measuring instrument. What’s the difference? and how is the “true” value defined?
There are deep philosophical questions and choices underlying this distinction, and it would take a whole university course to do them justice.
Intuitively we define the “true” value as the value that would be measured with an instrument that is perfectly calibrated and as precise as theoretically possible. If we make a distinction between such value and the currently measured value then we’re implying that the current measurement is made with a less precise instrument, and the true and measured values could be different.
In some circumstances this distinction is unimportant: an agent can use the “measured” value without worries, and consider it as the “true” one. Typically this is the case when the possible discrepancy between measured and true value is enough small to have no consequences. In other circumstances the discrepancy is important: slightly different values lead to quite different consequences. Then it is necessary for the agent to try to infer – using the probability calculus – the true value, using the measured one as “data” or “evidence”. Said otherwise, the agent doesn’t use the measured value directly, but only as an intermediate step to guess the true value. The latter, in turn, can be used for further inferences.
From the point of view of inference and decision-making, this distinction doesn’t lead to anything methodologically new: it just means that an agent has to do a chain of inferences instead of just one, using the four rules of inference as usual. This situation often requires the definition of two distinct quantities, the “true” and the “observed”, which can have slightly different domains. For instance we could have a voltage \(V_\text{obs}\) measured with rounding to \(1\,\mathrm{V}\) and therefore with discrete domain \(\set{10\,\mathrm{V}, 11\,\mathrm{V}, 12\,\mathrm{V}, \dotsc}\); while needing the “true” voltage \(V_\text{true}\) with a precision of at least \(0.01\,\mathrm{V}\), so this latter quantity could have a continuous domain.
In solving data-science and engineering problems it’s important to make clear whether a particular quantity value can be considered “true” and used as-is, or only “observed” with insufficient precision and used as data to infer the true value.